Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2748 problemas y 1042 soluciones.
Problema 814
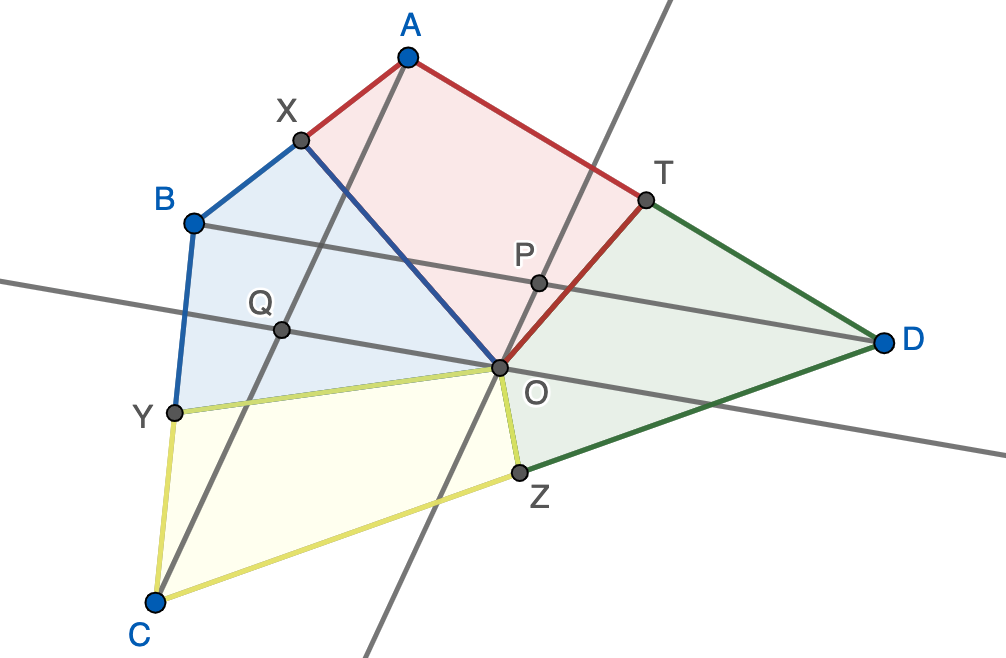
Sea $ABCD$ un cuadrilátero cualquiera. Sean $P$ y $Q$ los puntos medios de las diagonales $BD$ y $AC$, respectivamente. Las paralelas por $P$ y $Q$ a la otra diagonal se cortan en $O$. Si unimos $O$ con las cuatro puntos medios de los lados $X$, $Y$, $Z$ y $T$ se forman cuatro cuadriláteros: $OXBY$, $OYCZ$, $OZDT$ y $OTAX$. Probar que los cuatro cuadriláteros tienen la misma área.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 809
En un triángulo $ABC$, sean $A’$ el pie de la altura relativa al vértice $A$ y $H$ el ortocentro.
- Dado un número real positivo $k$ tal que $\frac{AA'}{HA'}=k$, encontrar la relación entre los ángulos $B$ y $C$ en función de $k$.
- Si $B$ y $C$ son fijos, hallar el lugar geométrico del vértice $A$ para cada valor de $k$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 805
Dos circunferencias secantes $C_1$ y $C_2$ de radios $r_1$ y $r_2$ se cortan en los puntos $A$ y $B$. Por $B$ se traza una recta variable que corta de nuevo a $C_1$ y $C_2$ en dos puntos que llamaremos $P_r$ y $Q_r$, respectivamente. Demostrar que existe un punto $M$ que depende solo de $C_1$ y $C_2$ tal que la mediatriz del segmento $P_rQ_r$ pasa por $M$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 802
Las rectas $r$ y $s$ son tangentes a la parábola de ecuación $y=x^2$ en los puntos $A$ y $B$ y se cortan en un punto $C$. La mediana del triángulo $ABC$ correspondiente al vértice $C$ tiene longitud $m$. Determinar el área del triángulo $ABC$ en función de $m$.
pistasolución 1info
Pista. Pon coordenadas $A=(a,a^2)$ y $B=(b,b^2)$ y calcula todos los elementos necesarios en función de $a$ y $b$.
Solución. Supongamos que los puntos son $A=(a,a^2)$ y $B=(b,b^2)$ con $a\lt b$. Teniendo en cuenta que la derivada de $x^2$ es $2x$, podemos calcular las expresiones $y=2ax-a^2$ e $y=2bx-b^2$ de las rectas tangentes. Es fácil resolver el sistema para obtener que estas tangentes se cortan en el punto $C=(\frac{a+b}{2},ab)$. Por otro lado, el punto medio de $AB$ es $M=(\frac{a+b}{2},\frac{a^2+b^2}{2})$, luego la recta $CM$ tiene ecuación $x=\frac{a+b}{2}$ (se trata de una recta vertical). El área de $ABC$ es el área de $BCM$ más el área de $ACM$, que pueden calcularse como un medio de la mediana $m=CM$ por las alturas respecto de este lado, que son rectas horizontales. Estas alturas son, de hecho, la diferencia de las primeras coordenadas de $B$ y $M$ y de $A$ y $M$. Tenemos entonces que el área que nos piden es
\[\mathrm{Área}(ABC)=\mathrm{Área}(BCM)+\mathrm{Área}(ACM)=\tfrac{1}{2}m(b-\tfrac{a+b}{2})+\tfrac{1}{2}m(\tfrac{a+b}{2}-a)=\tfrac{1}{2}m(b-a).\]
Ahora bien, tenemos también que $m=\frac{a^2+b^2}{2}-ab=\frac{1}{2}(b-a)^2$, de donde podemos despejar $b-a=\sqrt{2m}$. Con todo esto, podemos expresar el área únicamente en función de $m$ como nos piden:
\[\mathrm{Área}(ABC)=\frac{\sqrt{2}}{2}m^{3/2}.\]
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 799
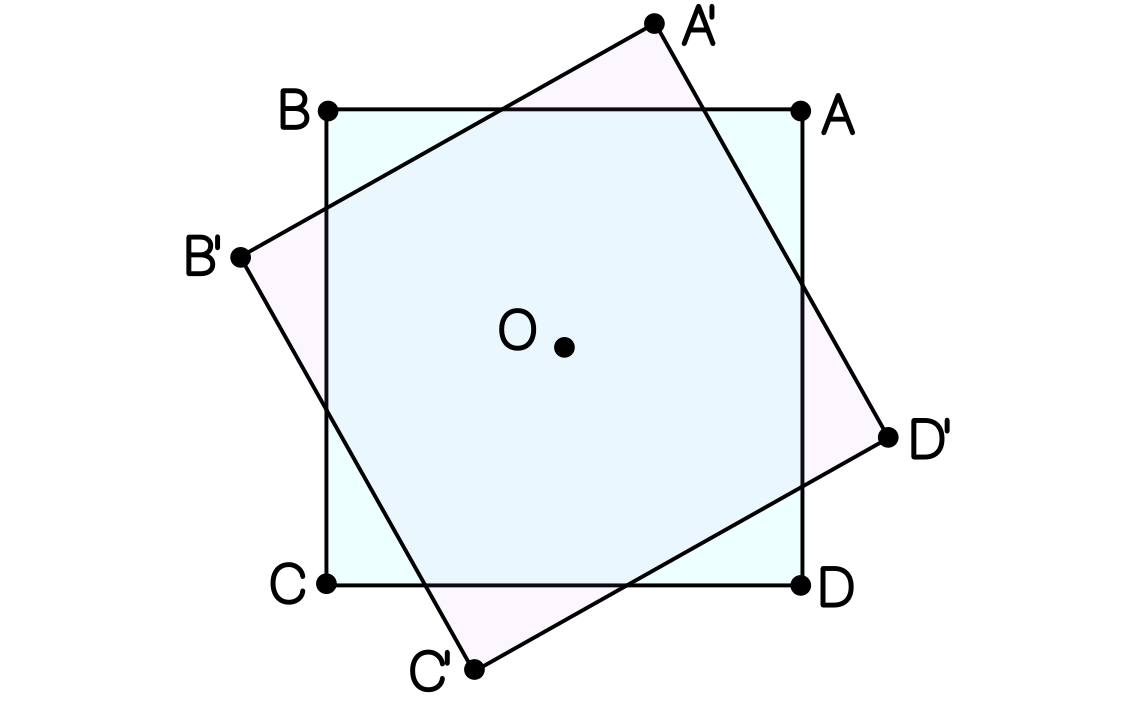
Un cuadrado $ABCD$ de lado $1$ gira un ángulo $\alpha$ en torno a su centro $O$. Hallar el área común a ambos cuadrados.
pistasolución 1info
Pista. El octógono se descompone en $8$ triángulos congruentes de altura $\frac{1}{2}$. Calcula la base correspondiente en términos de $\alpha$.
Solución. Consideremos los puntos $P$ y $Q$ indicados en la figura de abajo. Por simetría, el área se descompone en $8$ triángulos congruentes a $OPQ$. Este último triángulo, sombreado en la figura, tiene base $PQ$ y altura $\frac{1}{2}$, luego el área que nos piden es $S=8\cdot\frac{1}{2}\cdot\frac{1}{2}\cdot PQ=2 PQ$ y será suficiente calcular la longitud de $PQ$ en función de $\alpha=\angle A'PQ$.
Por la simetría de la figura y usando trigonometría en el triángulo $A'PQ$, obtenemos que $BP=A'P=PQ\cos\alpha$. Análogamente, tenemos que $AQ=A'Q=PQ\operatorname{sen}\alpha$, con lo que
\[1=AB=AQ+PQ+BP=PQ(1+\operatorname{sen}\alpha+\cos\alpha).\]
Esto nos lleva a la solución del problema
\[S=2PQ=\frac{2}{1+\operatorname{sen}\alpha+\cos\alpha}.\]
Nota. La solución presupone que $\alpha\in[0,90]$ implícitamente. Para un valor de $\alpha$ general, por la simetría de la construcción basta reducirlo módulo $90$ a un ángulo de dicho intervalo.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2025. Esta página ha sido creada mediante software libre