Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Consideremos los puntos $P$ y $Q$ indicados en la figura de abajo. Por simetría, el área se descompone en $8$ triángulos congruentes a $OPQ$. Este último triángulo, sombreado en la figura, tiene base $PQ$ y altura $\frac{1}{2}$, luego el área que nos piden es $S=8\cdot\frac{1}{2}\cdot\frac{1}{2}\cdot PQ=2 PQ$ y será suficiente calcular la longitud de $PQ$ en función de $\alpha=\angle A'PQ$.

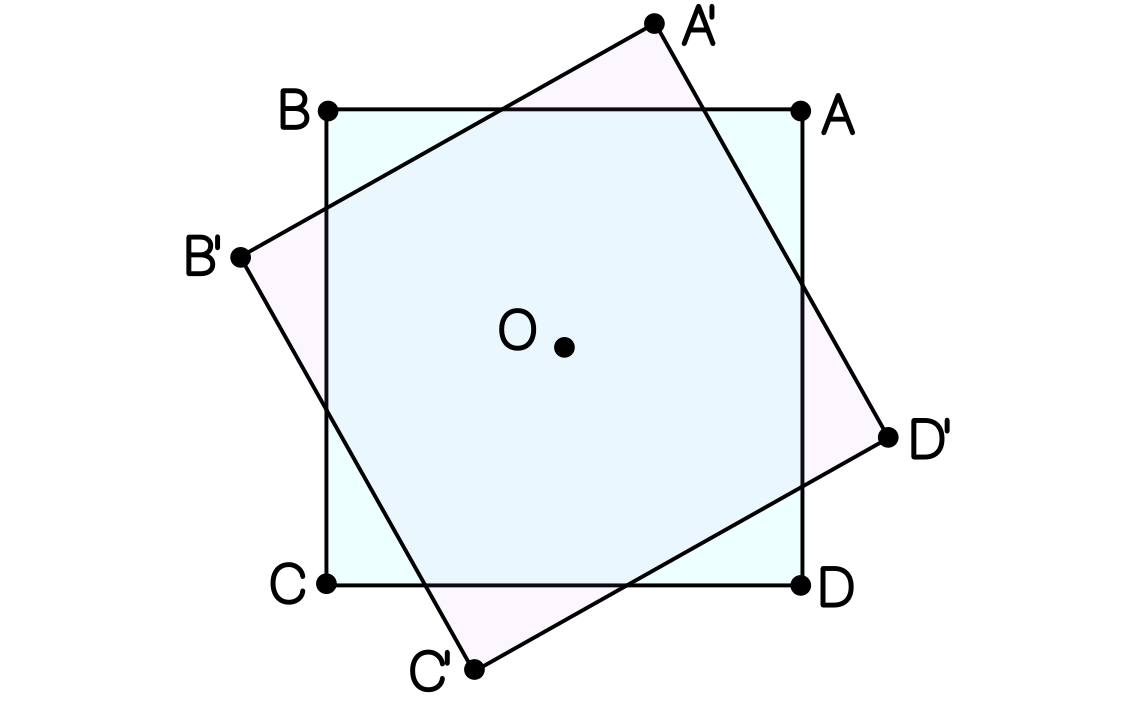
Por la simetría de la figura y usando trigonometría en el triángulo $A'PQ$, obtenemos que $BP=A'P=PQ\cos\alpha$. Análogamente, tenemos que $AQ=A'Q=PQ\operatorname{sen}\alpha$, con lo que \[1=AB=AQ+PQ+BP=PQ(1+\operatorname{sen}\alpha+\cos\alpha).\] Esto nos lleva a la solución del problema \[S=2PQ=\frac{2}{1+\operatorname{sen}\alpha+\cos\alpha}.\]

Nota. La solución presupone que $\alpha\in[0,90]$ implícitamente. Para un valor de $\alpha$ general, por la simetría de la construcción basta reducirlo módulo $90$ a un ángulo de dicho intervalo.

Solución. En la figura pueden verse los tres triángulos que tienen su vértice en $P$ dibujados de colores distintos. Trasladamos dos de ellos de forma paralela a los lados hasta que se apoyen los tres sobre un mismo lado del triángulo (en la figura hemos elegido el lado $AB$). Los tres triángulos así obtenidos son semejantes pues tienen sus lados paralelos a los lados del triángulo original. Por tanto, sus áreas serán proporcionales al cuadrado de sus alturas, es decir, $S_1=\lambda h_1^2$, $S_2=\lambda h_2^2$, $S_3=\lambda h_3^2$ para cierta constante positiva $\lambda$. Por otro lado, la altura del triángulo grande $ABC$ es $h_1+h_2+h_3$ y también es semejante a los tres triángulos pequeños, luego $S=\lambda(h_1+h_2+h_3)^2$ y la desigualdad a probar se puede reescribir como \[(h_1+h_2+h_3)^2\leq 3(h_1^2+h_2^2+h_3^2)\] ya que podemos cancelar $\lambda$ en ambos miembros. Desarrollando el cuadrado y agrupando términos, esta desigualdad se puede reescribir como \[0\leq 2(h_1^2+h_2^2+h_3^2-h_1h_2-h_1h_3-h_2h_3)=(h_1-h_2)^2+(h_2-h_3)^2+(h_3-h_1)^2,\] que es obviamente cierta.

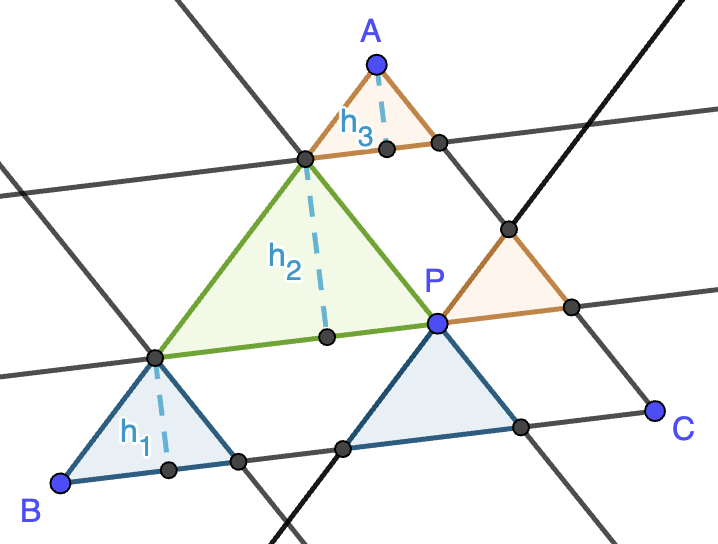
Nota. La igualdad se cumple cuando $h_1=h_2=h_3$, luego los tres triángulos pequeños deben ser iguales (congruentes). Esto se cumple si y solo si $P$ es el baricentro del triángulo. ¿Sabrías demostrarlo?

Solución. Si los cuatro puntos se quedaran a un mismo lado de un plano ecualizador, entonces serían coplanarios (estarían en un plano paralelo al ecualizador). Por tanto, un plano ecualizador debe separar a los cuatro puntos en $2$ y $2$ o bien $3$ y $1$. Para cada partición de los cuatro puntos en dos parejas, existe el plano ecualizador: basta tomar un plano paralelo a las rectas que contienen a sendas parejas y que las deje a la misma distancia (dicho plano es único porque las rectas no pueden ser paralelas ya que los cuatro puntos serían coplanarios. También para cada partición de los cuatro puntos en $3$ y $1$ puntos existe un único plano ecualizador ya que hay que tomarlo paralelo al plano que define el subconjunto de $3$ puntos y equidistante de este plano y del cuarto punto.

Por tanto, tenemos tantos planos ecualizadores como particiones: hay $3$ particiones de $2+2$ puntos y $4$ particiones de $3+1$ puntos, lo que nos da un total de $7$ planos ecualizadores.

Solución. Consideremos un triángulo $ABC$, su circuncentro $O$ y su ortocentro $H$. Si llamamos $M$ al punto medio del lado $BC$, tendremos que demostrar que $AH=2BC$. Para ello, trazamos el diámetro de la circunferencia circunscrita que pasa por $B$ y su punto diametralmente opuesto, que llamaremos $P$, como se indica en la figura. Por ser $BP$ un diámetro, se tiene que $PC$ es perpendicular a $BC$ y, por tanto, paralela a la mediatriz $OM$. Entonces, los triángulos $BOM$ y $BPC$ son semejantes y se cumple que $PC=2OM$, luego tendremos que demostrar que $PC=AH$. Esto último se sigue de que $APCH$ es un paralelogramo ya que $PC$ es paralela a la altura $AH$ y $AP$ es paralela a la altrua $CH$ (ya que el ángulo $\angle BAP$ es recto por comprender al diámetro $BP$).

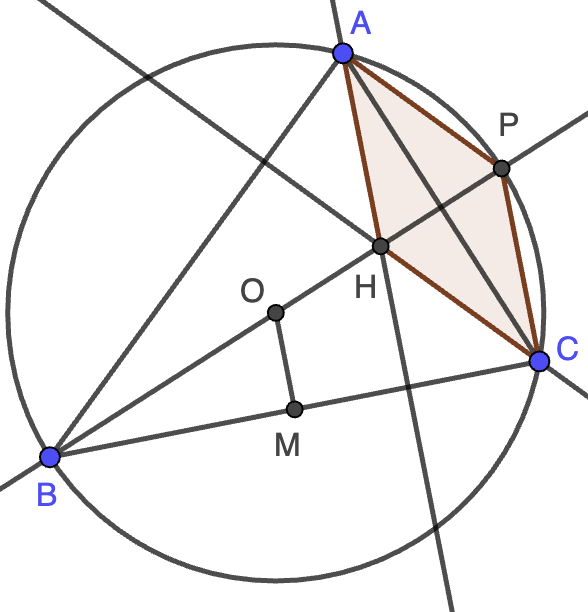
Nota. Este es un resultado relativamente conocido en el ámbito de la geometría de olimpiadas. ¿Sabrías probar que $AH=2R\cos A$ y $OM=R\cos A$, siendo $R$ el radio de la circunferencia circunscrita? ¿Sabrías probar a partir de este resultado que las rectas $OA$ y $MH$ se cortan en un punto de la circunferencia circunscrita?