Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 771
Sea $ABC$ un triángulo rectángulo isósceles con el ángulo recto en $C$ y los catetos de longitud $2$. Un arco de círculo $\ell$ con centro $A$ divide al triángulo en dos partes de la misma área, mientras que el arco de círculo $m$ con centro en $B$ es tangente a $\ell$ en un punto de la hipotenusa $AB$. Hallar el área de la porción del triángulo no cubierta por los sectores circulares correspondientes a los dos arcos.
pistasolución 1info
Pista. Calcula primero el radio del arco $\ell$ y luego el radio del arco $m$, con lo que podrás calcular el área de los sectores circulares.
Solución. El área del triángulo es $2$ y el área del sector circular de arco $\ell$ (en azul en la figura) es $\frac{1}{8}\pi r^2$, siendo $r$ su radio. Esto viene de que es un octavo del círculo de radio $r$ ya que el ángulo $A$ del triángulo rectángulo isósceles $ABC$ es $45^\circ$. Igualando a la mitad del área del triángulo, obtenemos
\[\tfrac{1}{8}\pi r^2=1\ \Longleftrightarrow\ r=2\sqrt{\tfrac{2}{\pi}}.\]
Observamos que $r\lt 2$, lo que nos dice que el sector realmente está bien definido. Ahora bien, el radio $s$ del sector de arco $m$ (en naranja en la figura) sumado con $r$ nos da la hipotenusa $AB=2\sqrt{2}$, luego podemos despejar
\[s=AB-r=2\sqrt{2}-2\sqrt{\tfrac{2}{\pi}}=2\sqrt{2}(1-\tfrac{1}{\sqrt{\pi}}).\]
Tenemos entonces que el área que nos piden (en verde en la figura) es
\[2-\tfrac{\pi}{8}r^2-\tfrac{\pi}{8}s^2=2-1-\tfrac{8\pi}{8}(1-\tfrac{1}{\sqrt{\pi}})^2=2\sqrt{\pi}-\pi.\]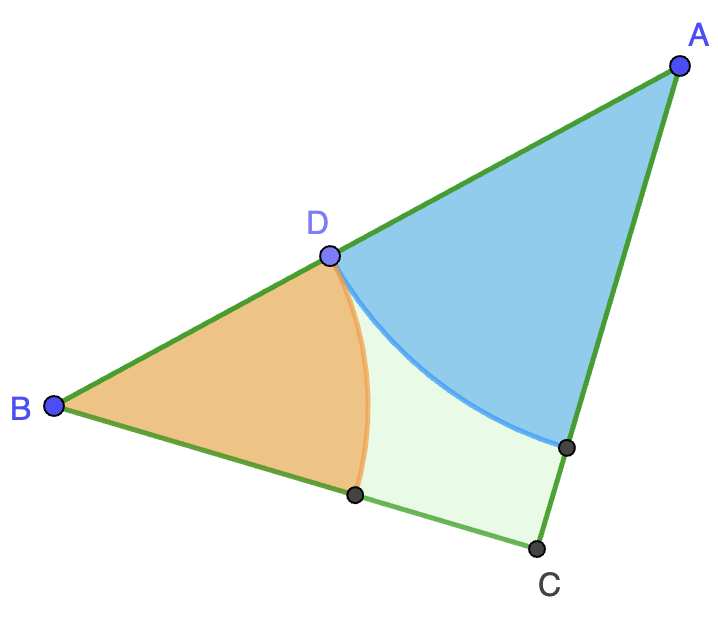

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 768
OIM, 2003-P5
En el cuadrado $ABCD$, sean $P$ y $Q$ puntos pertenecientes a los lados $BC$ y $CD$, respectivamente, distintos de los extremos y tales que $BP=CQ$. Se consideran puntos $X$ e $Y$, $X\neq Y$, pertenecientes a los segmentos $AP$ y $AQ$, respectivamente. Demuestre que, cualesquiera que sean $X$ e $Y$, existe un triángulo cuyos lados tienen las longitudes de $BX$, $XY$ y $DY$.
pistasolución 1info
Pista. Dobla el papel en el que has dibujado el cuadrado.
Solución. Si recortamos el cuadrado y también el triángulo $CPQ$, podemos doblar por las líneas $AP$ y $AQ$ para formar una pirámide con vértice en $A$. Observemos que, de esta forma $B$ se identifica con $D$ ya que ambos puntos están a la misma distancia de $A$. No obstante, para comprobar que efectivamente la pirámide se cierra, observamos que el triángulo de vértices $B=D$, $P$ y $Q$ en el espacio es rectángulo ya que es congruente con el triángulo $CPQ$ que hemos quitado. Ahora la solución al problema es evidente ya que $BX$, $XY$ y $DY$ forman un triángulo en el espacio.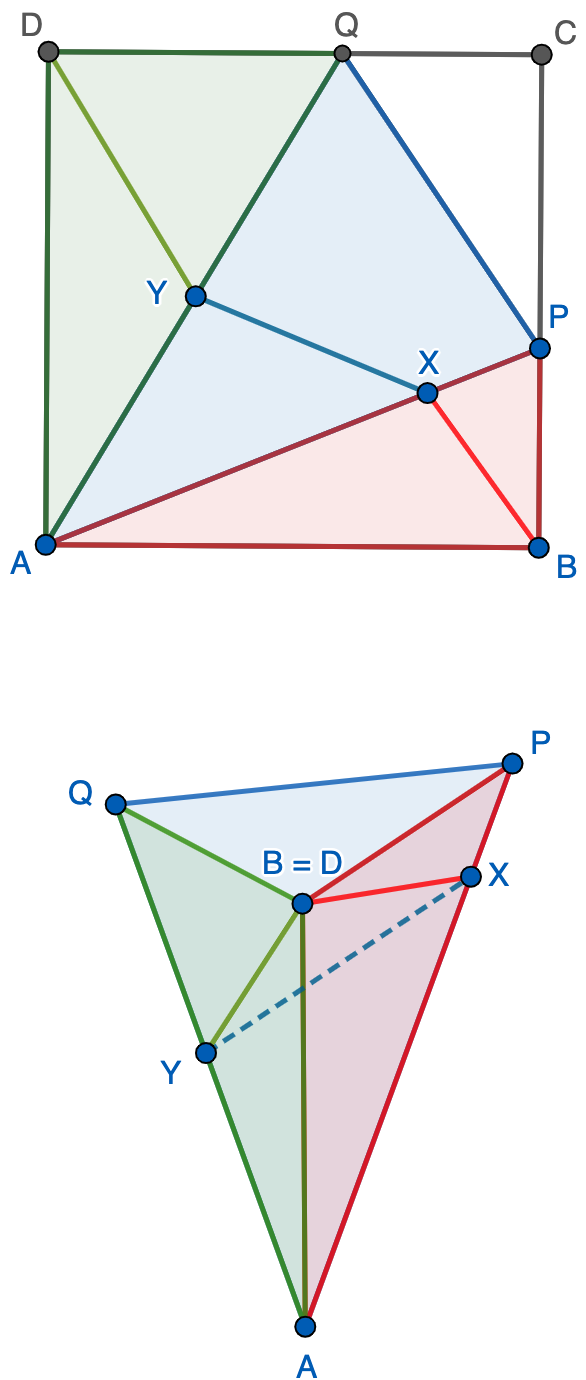

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 767
OIM, 2003-P2
Sean $C$ y $D$ dos puntos de la semicircunferencia de diámetro $AB$ tales que $B$ y $C$ están en semiplanos distintos respecto de la recta $AD$. Denotemos por $M$, $N$ y $P$ los puntos medios de $AC$, $DB$ y $CD$, respectivamente. Sean $O_A$ y $O_B$ los circuncentros de los triángulos $ACP$ y $BDP$. Demostrar que las rectas $O_AO_B$ y $MN$ son paralelas.
pistasolución 1info
Pista. Demuestra que $OO_AO_B$ y $OMN$ son semejantes, siendo $O$ el centro de la semicircunferencia. Te puede ser útil utilizar el teorema de Thales.
Solución. Las mediatriz de $AC$ pasa por $O_A$ y por el centro $O$ de la semicircunferencia y, de la misma forma, la mediatriz de $BD$ pasa por $O_B$ y por $O$. Por tanto, que $O_AO_B$ sea paralela a $MN$ equivale a que los triángulos $OO_AO_B$ y $OMN$ sean semejantes. Si trazamos perpendiculares a la recta $CD$ que pasan por $A$, $M$, $O_A$, $O_B$, $N$ y $B$ (en línea discontinua en la figura) y marcamos los puntos de intersección con $CD$ como $E$, $F$, $G$, $H$, $I$ y $J$, respectivamente, el teorema de Thales nos dice que
\[\frac{OO_A}{GP}=\frac{OM}{PF},\qquad \frac{OO_B}{HP}=\frac{ON}{PI}.\]
Utilizando que $G$ y $H$ son los puntos medios de $CP$ y $DP$ (ya que las perpendiculares por $O_A$ y $O_B$ son mediatrices de $CP$ y $DP$, respectivamente), las semejanzas anteriores se reescriben como
\[\frac{OO_A}{OM}=\frac{CP}{2PF},\qquad \frac{OO_B}{ON}=\frac{DP}{2PI}.\]
Como $CP=DP$ por ser $P$ el punto medio de $CD$, el problema estará resuelto si demostramso que $PF=PI$. Usando de nuevo que $CP=DP$, podemos reducir el problema aún más a probar que $PE=PJ$, pero esto último es sencillo ya que es consecuencia del teorema de Thales aplicado a las paralelas $BJ$, $OP$ y $AE$ que cortan a las rectas $AB$ y $AJ$, teniendo en cuenta que $O$ es el punto medio de $AB$.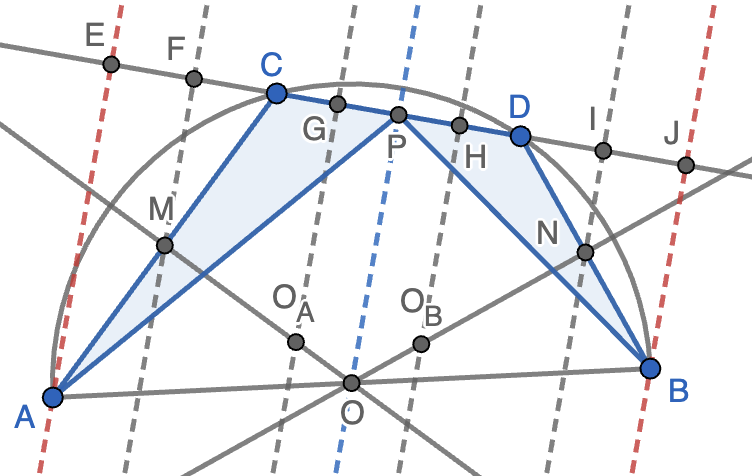

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 764
OIM, 2002-P4
En un triángulo escaleno $ABC$ se traza la bisectriz interior $BD$, con $D$
sobre $AC$. Sean $E$ y $F$, respectivamente, los pies de las perpendiculares trazadas desde $A$ y $C$ hacia la recta $BD$ y $M$ el punto sobre el lado $BC$ tal que $DM$ es perpendicular a $BC$. Demostrar que $\angle EMD=\angle DMF$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 763
OIM, 2002-P3
Un punto $P$ interior al triángulo equilátero $ABC$ es tal que $\angle APC=120^\circ$. Sean $M$ la intersección de $CP$ con $AB$ y $N$ la intersección de $CP$ con $BC$. Hallar el lugar geométrico del circuncentro del triángulo $MBN$ al variar $P$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre