Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
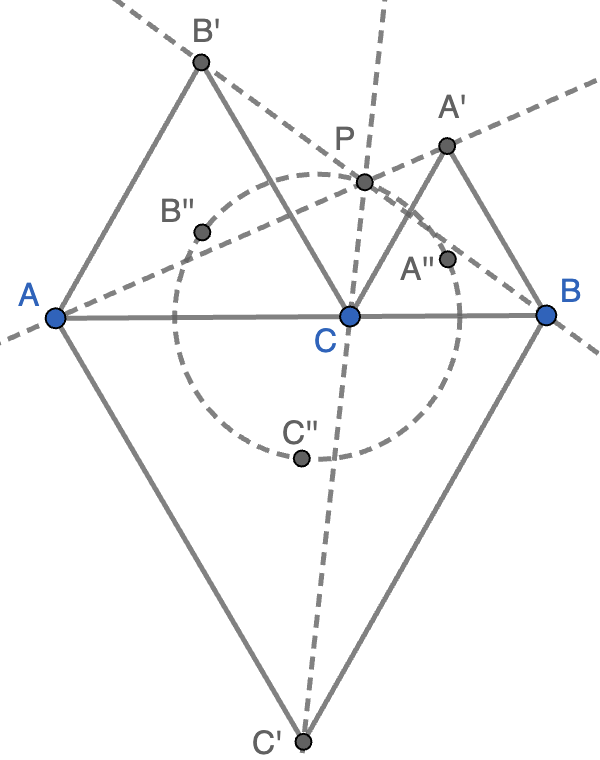
- Demostrar que las rectas $AA'$, $BB'$ y $CC'$ tiene un punto común $P$.
- Hallar el lugar geométrico de $P$ cuando $C$ varía en el segmento $AB$.
- Demostrar que los centros $A''$, $B''$ y $C''$ de los tres triángulos equiláteros forman a su vez un triángulo equilátero.
- Demostrar que los puntos $A''$, $B''$, $C''$ y $P$ están sobre una circunferencia.
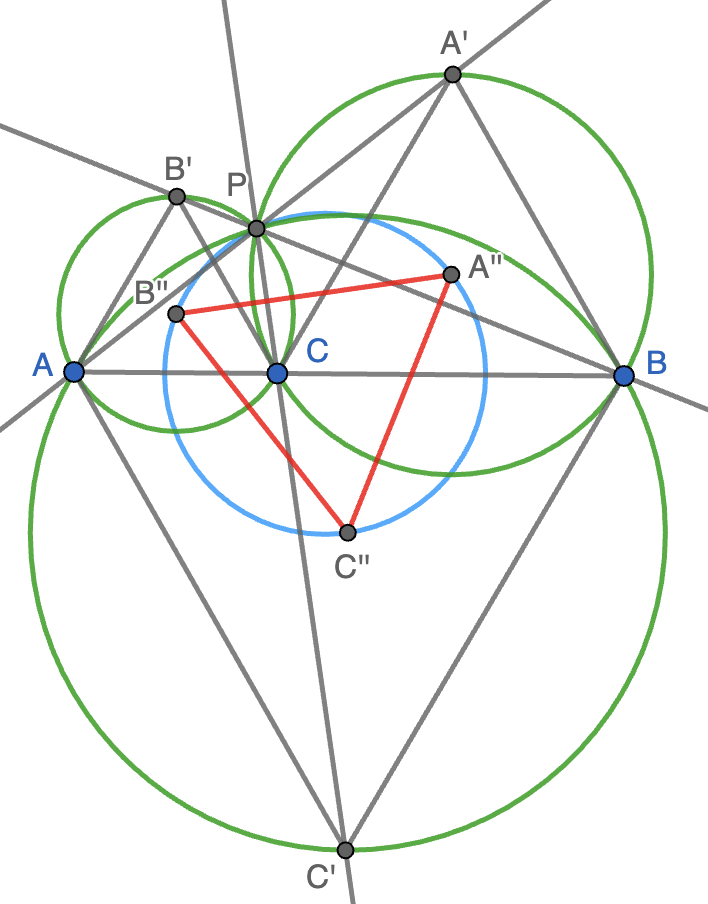
Observemos que, como $A'',B'',C''$ son los centros de las circunferencias circunscritas que hemos trazado, se cumple que la recta $A''B''$ es perpendicular a la recta $CC'$, la recta $A''C''$ es perpendicular a $BB'$ y la recta $B''C''$ es perpendicular a $AA'$. Como las rectas $AA',BB',CC'$ forman ángulos de $60^\circ$, obtenemos que $A''B'',B''C'',C''A''$ también forman ángulos de $60^\circ$, luego el triángulo $A'',B'',C''$ es equilátero y tenemos ya el apartado (c).
Finalmente, para responder al apartado (d), consideremos el punto $Q$ diametralmente opuesto a $P$ en la circunferencia circunscrita a $AB'C$. Se tiene entonces que $\angle PB'Q=90^\circ$ y $\angle AB'P=120^\circ$, luego, una vez más por la propiedad del arco capaz, \[\angle B'PB''=\angle B'PQ=90^\circ-\angle B'QP=90^\circ-\angle B'CP.\] De la misma forma, se tiene que $\angle A'PA''=90^\circ-\angle A'CP$, luego podemos sumar para obtener que \[\angle B'PB''+\angle A'PA''=180-\angle B'CP-\angle A'CP=180^\circ-\angle B'CA'=120^\circ.\] Como $\angle B'PB''+\angle B''PA''+\angle A'PA''=240^\circ$, obtenemos que $\angle B''PA''=120^\circ$, luego $P$ está en la circunferencia circunscrita al triángulo $A''B''C''$.
Nota. El problema en sí está muy relacionado con el teorema de Napoleón para el triángulo $ABC$. Justo nos dicen que analicemos el caso en que $ABC$ es degenerado (sus vértices están alineados). Los apartados (a), (b) y (c) son parte de la demostración estándar de este resultado clásico, aunque (d) es distinto ya que no es cierto en general para un triángulo cualquiera.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
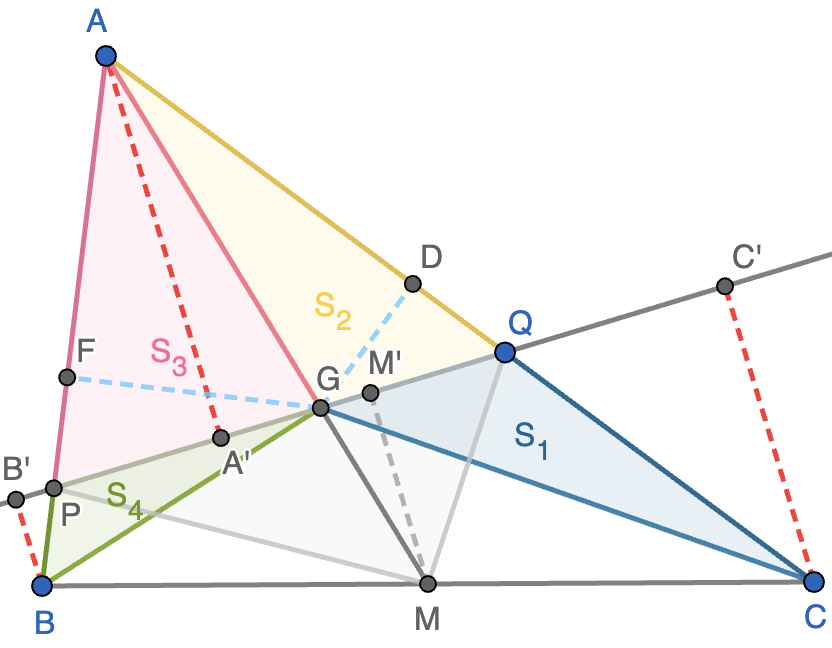
- Calcular las medidas de los ángulos del triángulo $BCD$.
- Expresar la medida del lado $BC$ en función de la medida del lado $AC$, sin que en la expresión aparezcan razones trigonométricas.
El triángulo $ABD$ también es isósceles por tener dos ángulos iguales a $36^\circ$, luego $BC=BD=AD$. Además, $BCD$ y $ABC$ son semejantes por tener los ángulos iguales, luego
\[\frac{AC}{BC}=\frac{BC}{CD}=\frac{BC}{AC-AD}=\frac{BC}{AC-BC}.\]
De esta igualdad, obtenemos que $AC^2-AC\cdot BC-BC^2=0$. Dividiendo entre $AC^2$, llegamos a la ecuación de segundo grado
\[\left(\frac{BC}{AC}\right)^2+\frac{BC}{AC}-1=0\ \Longrightarrow\ \frac{BC}{AC}=\frac{-1\pm\sqrt{5}}{2}.\]
Tenemos que descartar la solución negativa, lo que nos dice finalmente que
\[BC=\frac{\sqrt{5}-1}{2}AC.\]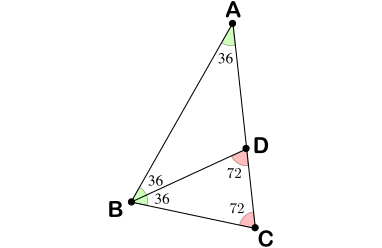
Informar de error en enunciado Informar de procedencia del problema