Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
Resta por ver si este triángulo cumple la propiedad. De nuevo por el teorema del coseno, tenemos que el ángulo $\alpha$ opuesto al lado de longitud $4$ cumple \[\cos(\alpha)=\frac{5^2+6^2-4^2}{2\cdot 5\cdot 6}=\frac{3}{4}.\] Por su parte, el ángulo $\beta$ opuesto al lado de longitud $6$ cumple \[\cos(\beta)=\frac{4^2+5^2-6^2}{2\cdot 4\cdot 5}=\frac{1}{8}=2\cos^2(\alpha)-1=\cos(2\alpha).\] Deducimos que $\beta=2\alpha$, luego en este triángulo el ángulo mayor es el doble del menor y respondemos así afirmativamente a la pregunta del enunciado.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
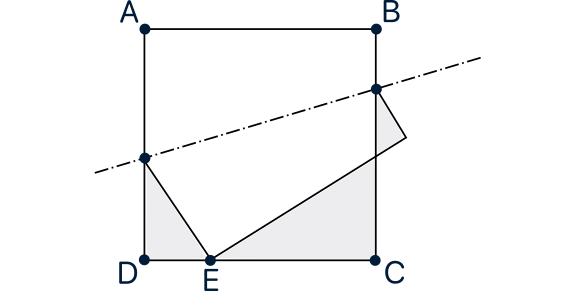
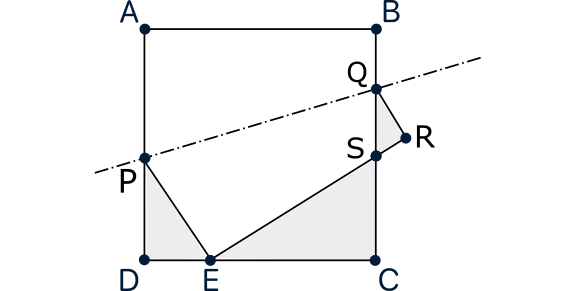
Los triángulos sombreados $PDE$, $SCE$ y $SRQ$ son semejantes (son rectángulos y es muy fácil ver que tienen otro ángulo igual). Como $EC=1-DE=1-x$ se corresponde en la semejanza con $PD= \frac{1-x^2}{2}$, el factor de proporcionalidad para pasar de $PDE$ a $SCE$ es $\frac{2}{1+x}$, luego deducimos que $SCE$ tiene perímetro $2$ (la mitad del perímetro del cuadrado, lo que responde a una de las preguntas del enunciado. Así, las longitudes de los lados de $SCE$ (nos las piden también en el enunciado) son \[CE=\frac{2x}{1+x},\qquad SC=1-x,\qquad SE=\frac{1+x^2}{1+x}.\] Ahora observamos que $SR=1-SE=\frac{x(1-x)}{1+x}$. Como este lado se corresponde con $SC=1-x$ en la semejanza, tenemos que el factor de semejanza para pasar de $SCE$ a $SRQ$ es $\frac{1-x}{2}$, por lo que el perímetro de $SRQ$ es $2\cdot \frac{1-x}{2}=1-x$ y sus lados vienen dados por \[RQ=\frac{x(1-x)}{1+x},\qquad SR=\frac{(1-x)^2}{2},\qquad SQ=\frac{(1+x^2)(1-x)}{2(1+x)}.\] La suma de los perímetros de $PDE$ y $SRQ$ es $(1+x)+(1-x)=2$, el perímetro de $SCE$, luego ya hemos demostrado todo lo que nos piden.
Informar de error en enunciado Informar de procedencia del problema
Pongamos $x=AC$ y $r=AO$. Entonces, $CO=r-x$ y el teorema de la altura en el triángulo rectángulo $ADO$ nos dice que $CD^2=AC\cdot CO=x(r-x)$, de donde $AD^2=AC^2+CD^2=x^2+x(r-x)=rx$ por el teorema de Pitágoras. De forma similar, en el triángulo rectángulo $AEO$, el teorema de la altura nos dice que $CE^2=AC\cdot CB=x(2r-x)$, luego
\[AE^2=AC^2+CE^2=x^2+x(2r-x)=2xr=2AD^2,\]
como queríamos probar.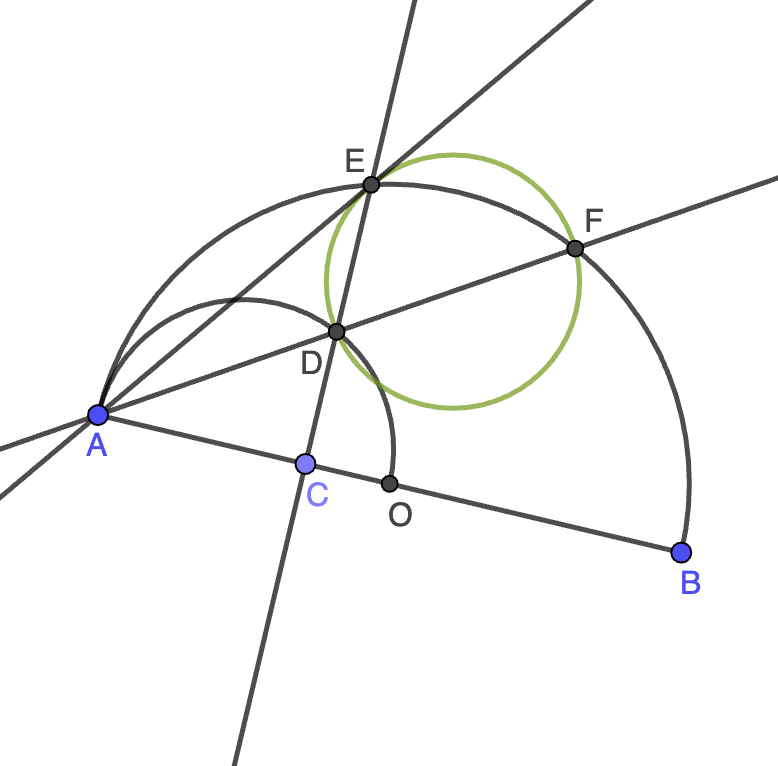
Informar de error en enunciado Informar de procedencia del problema