Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Supongamos que las longitudes de los lados son $a,ar,ar^2$ para $r\geq 1$. El triángulo en cuestión debe verificar la desigualdad triangular para existir. Como lados están ordenados de mayor a menor, también lo estarán los correspondientes lados opuestos, lo que nos lleva a que la desigualdad triangular equivale a $ar^2\gt a+ar$, es decir, $r^2-r-1\gt 0$. Esta desigualdad se resuelve fácilmente y nos dice que el dominio donde se mueve la variable $r$ es $1\leq r\lt\frac{1+\sqrt{5}}{2}$.

De vuelta al problema en cuestión, se trata de ver si el ángulo $\alpha$ opuesto a $ar^2$ es agudo, recto u obtuso. Por el teorema del coseno, este ángulo verifica \[(ar^2)^2=a^2+(ar)^2-2a(ar)\cos(\alpha)\ \Leftrightarrow\ \cos(\alpha)=\frac{1+r^2-r^4}{2r}\] y buscamos saber cuándo esta última cantidad es negativa (obtusángulo), cero (rectángulo) o positiva (acutángulo). Para ello, resolvemos la ecuación bicuadrada $1+r^2-r^4=0$, que nos da soluciones \[r^2=\frac{1\pm\sqrt{5}}{2}\ \Rightarrow\ r=\pm\sqrt{\frac{1+\sqrt{5}}{2}},\] donde hemos descartado las dos soluciones (complejas) en que $r^2$ era negativo. Deducimos que el polinomio $p(r)=1+r^2-r^4$ cambia de signo en estos dos valores (son raíces simples). Como el coeficiente de mayor grado es negativo, $p(r)$ pasa de negativo a positivo y luego a negativo. Tenemos así la solución al problema:

• acutángulo: $1\leq r\lt \sqrt{\frac{1+\sqrt{5}}{2}}$,
• rectángulo: $r=\sqrt{\frac{1+\sqrt{5}}{2}}$,
• obtusángulo: $\sqrt{\frac{1+\sqrt{5}}{2}}\lt r\lt \frac{1+\sqrt{5}}{2}$.

Solución. Sean $A$ y $B$ los dos vértices más alejados entre sí del polígono y consideramos los dos vértices $C$ y $D$ más alejados de la recta $AB$ en sendos semiespacios definidos por $AB$. Trazamos por $A$ y $B$ perpendiculares $r_A$ y $r_B$ a $AB$ y por $C$ y $D$ paralelas $r_C$ y $r_D$ a $AB$. Estas cuatro rectas $r_A,r_B,r_C,r_D$ determinan un rectángulo $R$. Vamos a ver que $R$ (que es, en particular, paralelogramo) contiene al polígono y que tiene área menor o igual que $2$.

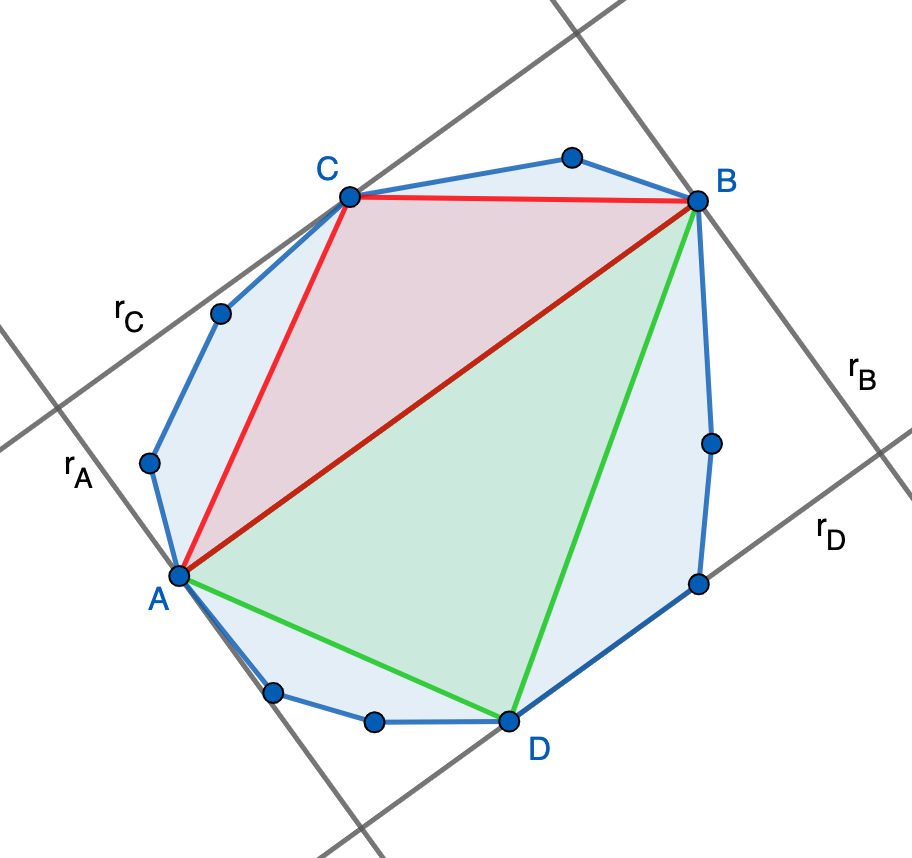
• En primer lugar, tenemos que ningún vértice se puede salir de la banda determinada por $r_A$ y $r_B$ ya que en tal caso dicho vértice tendría distancia con $A$ o con $B$ mayor que $AB$ (¿por qué?), contradiciendo que $AB$ es el segmento entre vértices de longitud máxima. Por otro lado, ningún vértice se puede salir de la banda determinada por $r_C$ y $r_D$ ya que en tal caso dicho vértice distaría de $AB$ más que $C$ o $D$, contradiciendo que estos son los puntos más alejados. Por tanto, todos los vértices del polígono están en $R$ y, por convexidad, todo el polígono debe estar en $R$.
• Finalmente, veamos que $\text{área}(R)\leq 2$. Para ello, observamos que los triángulos $ACB$ y $ADB$ están contenidos en el polígono (de nuevo, por convexidad), de donde \[1=\text{área}(\text{polígono})\geq\text{área}(ACB)+\text{área}(ADB)=\tfrac{1}{2}\text{área}(R).\]

Esto termina la demostración. Es importante observar que uno de los dos puntos $C$ o $D$ podría no estar definido porque no haya vértices a un lado de la recta $AB$. En tal caso, se razona de forma similar usando que $r_C=AB$ o $r_D=AB$.

Solución. Consideremos la circunferencia $\Gamma'$ que surge al trasladar $\Gamma$ una distancia $h$ en vertical. El problema equivale a encontrar una recta horizontal que corte a $\Gamma$ y $\Gamma'$ en sendos segmentos cuya suma de longitudes sea precisamente $m$ (el segmento correspondiente a $\Gamma$ es una de las bases del trapecio y el segmento correspondiente a $\Gamma'$ será la otra base después de trasladarlo $-h$ en vertical.

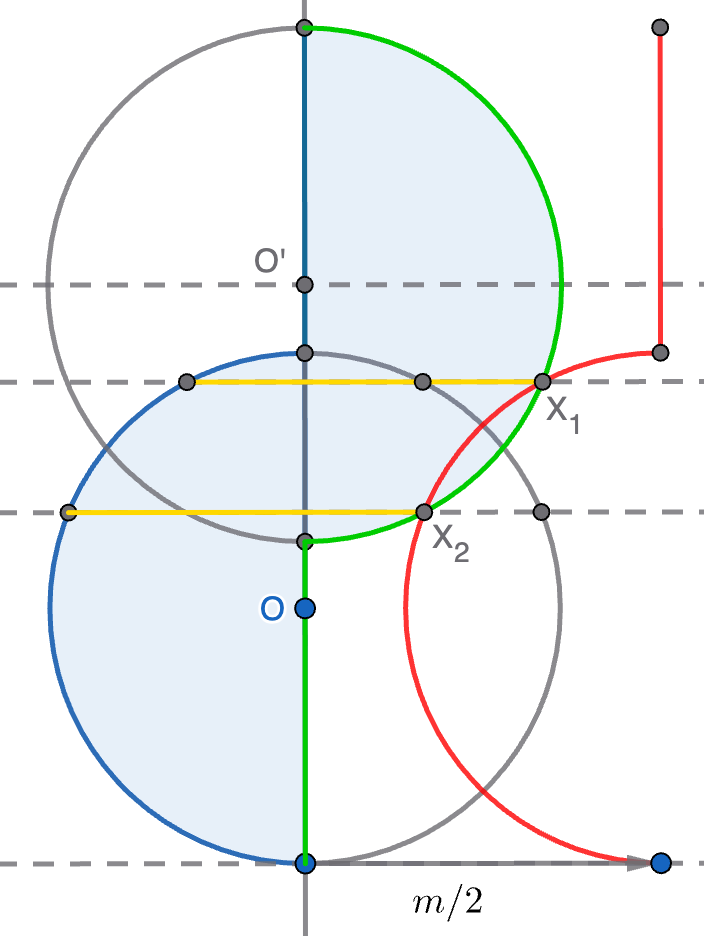
Consideremos entonces el eje de simetría vertical común a ambas circunferencias y nos quedamos con la semicircunferencia $S$ de $\Gamma$ a la derecha del eje y con la semicircunferencia $S'$ de $\Gamma'$ a la derecha del eje, delimitando ambas la región sombreada de la figura. Como nos hemos quedado con la mitad de cada circunferencia, ahora queremos ver qué recta horizontal corta a la zona sombreada en una longitud $\frac{m}{2}$. Para ello, movemos la figura $\frac{m}{2}$ a la derecha y vemos dónde corta el borde izquierdo trasladado (en rojo en la figura) al borde derecho original (en verde). Cada punto $X$ en la intersección nos da una posible solución que viene dada por la recta horizontal que pasa por $X$. En la figura se ha puesto un ejemplo en el que hay dos soluciones $X_1$ y $X_2$ que producen sendos segmentos de longitud $\frac{m}{2}$, indicados en amarillo.