Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. El radio inscrito del triángulo es igual a $\frac{1}{\sqrt{3}}$ y su radio circunscrito $\frac{2}{\sqrt{3}}$. Por lo tanto, podemos tomar coordenadas con centro en el centro del triángulo de forma que la circunferencia inscrita tenga ecuación $x^2+y^2=\frac{1}{3}$ y los vértices están sobre la circunferencia de centro el origen y radio $\frac{2}{\sqrt{3}}$. Podemos tomar entonces los tres vértices como \begin{align*} A&=\Bigl(\tfrac{2}{\sqrt{3}},0\Bigr),\\ B&=\tfrac{2}{\sqrt{3}}\left(\cos(120),\mathrm{sen}(120)\right)=\Bigl(\tfrac{-1}{\sqrt{3}},1\Bigr),\\ C&=\tfrac{2}{\sqrt{3}}\left(\cos(240),\mathrm{sen}(240)\right)=\Bigl(\tfrac{-1}{\sqrt{3}},-1\Bigr). \end{align*} Entonces, la suma de los cuadrados de un punto $P=(x,y)$ a los tres vértices se escribe como \[(x-\tfrac{2}{\sqrt{3}})^2+y^2+(x+\tfrac{1}{\sqrt{3}})^2+(y-1)^2+(x+\tfrac{1}{\sqrt{3}})^2+(y+1)^2=4+3(x^2+y^2)=5.\] siempre que $P$ esté en la circunferencia inscrita.

Que se puede formar un triángulo con los segmentos $AP,BP,CP$ es cierto para cualquier punto interior al triángulo. Observemos que podemos prolongar $AP$ hasta llegar a un punto $D$ del lado $BC$. Con lo que $AP\leq AD\leq BC\leq BP+PC$, donde hemos usado que la longitud de $AD$ es menor que la longitud de un lado y la desigualdad triangular. Se razona de la misma forma que $BP\leq AP+CP$ y que $CP\leq AP+BP$.

Para calcular el área del triángulo, llamemos $a=AP$, $b=BP$ y $c=CP$ por comodidad. La fórmula de Herón nos dice que \begin{align*} 16S^2&=(a+b+c)(-a+b+c)(a-b+c)(a+b-c)\\ &=((b+c)^2-a^2)((b-c)^2-a^2)\\ &=-a^4+2 a^2 b^2+2 a^2 c^2-b^4+2 b^2 c^2-c^4\\ &=4(a^2b^2+b^2c^2+c^2a^2)-(a^2+b^2+c^2)^2. \end{align*} Hemos probado que $a^2+b^2+c^2=5$ y también es fácil comprobar que \[a^2b^2+b^2c^2+c^2a^2=3(x^2+y^2)^2+4(x^2+y^2)+\tfrac{16}{3}=7,\] lo que nos lleva a que $16S^2=4\cdot 7-25=3$ y, por tanto, $S=\frac{\sqrt{3}}{4}$.

Solución. Renombraremos el punto $P$ como $H$, ya que se trata del ortocentro del triángulo. Supongamos que el triángulo $ABC$ ya está construido para tener intuición sobre cómo hacer la cosntrucción. Supongamos que $M$ es el punto medio de $AB$ y $N$ es el punto medio de $AC$. Si consideramos un punto $X$ tal que $AHBX$ es un paralelogramo, entonces $AX$ es paralela a $BH$ (que es una altura del triángulo) y, por tanto, perpendicular a $AC$. Por tanto, el triángulo $XAN$ es rectángulo en $A$ y $A$ debe estar sobre la circunferencia de diámetro $XN$. Por otro lado $A$ también debe estar en la perpendicular a $MN$ que pasa por $H$ (que es la altura del lado $A$). Esto nos permite determinar el punto $A$, a partir del cual se obtienen $B$ y $C$ rápidamente. El proceso de construcción es el siguiente (la construcción en cada paso es sencilla y se deja como ejercicio entender cómo se haría con regla y compás):

1. Se determina el punto $X$ tal que $M$ es el punto medio de $XH$.
2. Se traza la circunferencia de diámetro $XN$.
3. Se ubica el vértice $A$ en la intersección de dicha circunferencia con la perpendicular a $MN$ que pasa por $H$.
4. Se determinan los puntos $B$ y $C$ de forma que $M$ es el punto medio de $AB$ y $N$ es el punto medio de $AN$.

Ahora bien, puede ocurrir que la intersección de la recta y la circunferencia sea vacía, tenga un único punto o tenga dos puntos. Por el argumento previo, esto se corresponderá con que haya 0, 1 o 2 soluciones al problema. Se muestra en la figura un ejemplo en el que hay dos soluciones $A_1B_1C_1$ (en azul) y $A_2B_2C_2$ (en naranja).

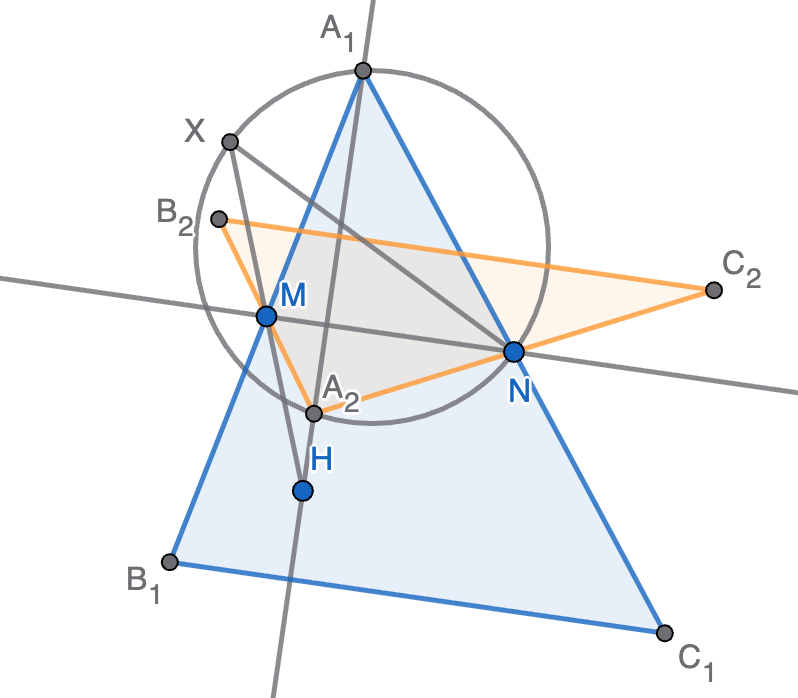
Nota. Sería interesante (como nuevo ejercicio), hallar condiciones sencillas sobre $M$, $N$ y $H$ para que exista solución.

Solución. Llamemos $A,B,C,D$ a las cuatro regiones en que el cuadrado queda dividido por las dos rectas, que llamaremos $r$ y $s$, como indica la figura. También supondremos que $A$, $B$ y $C$ son las regiones que tienen área $1$. Consideraremos la rotación de $90^\circ$ con centro en el centro $O$ del cuadrado y denotaremos por $A',B',C',D'$ a las regiones rotadas y por $r'$ y $s'$ a las rectas rotadas.

La región rotada $A'\cup B'$ tiene área $2$ y está delimitada por $r'$, mientras que $B\cup C$ está delimitada por $s$ paralela a $r'$ y también tiene área $2$. Para que esto ocurra, debe ser necesariamente $r'=s$ (en caso contrario, $A'\cup B'$ estaría estrictamente contenida en $B\cup C$ o viceversa, luego no podrían tener la misma área). Por un argumento similar, la región $B'$ debe coincidir con $C$ para que ambas tengan área $1$ (si no, $B'$ estaría estrictamente contenida en $C$ o viceversa). Por lo tanto, el punto de intersección de $r$ y $s$ debe ser el centro de rotación $O$. Así, $A,B,C,D$ son congruentes mediante rotaciones respecto de $O$ y tienen todas área $1$.

Solución. Sean $O_1$ y $O_2$ los centros de $C_1$ y $C_2$, respectivamente, y $r_1$ y $r_2$ sus radios. Si consideramos la recta $s$ paralela a $t$ a distancia $R_1$ y que no contiene a $O$, se tiene que la distancia de $O_2$ a $O_1$ es igual a $r_2+r_1$, que es la distancia de $O_2$ a $s$. Por lo tanto, el lugar geométrico de $O_2$ es una parábola que tiene por vértice $B$. Está claro además que $O_2O_1=r_2+r_1$ es la hipotenusa de un triángulo rectángulo de catetos $BP$ y $|r_1-r_2|$, de donde podemos despejar \[BP=\sqrt{(r_1+r_2)^2-(r_1-r_2)^2}=2\sqrt{r_1r_2},\] luego podemos determinar $P$ como el punto de $t$ que está a distancia $2\sqrt{r_1r_2}$ de $B$ y en la misma semirrecta en que se proyecta $O_2$.

Para responder al apartado (b), hacemos una inversión respecto de la circunferencia centrada en $B$ y de radio $2r_1$, que deja $t$ invariante y lleva $C_1$ en la recta $C_1'$ paralela a $t$ que pasa por $A$. Como las inversiones mantienen las rectas/circunferencias, los ángulos y las tangencias, la circunferencia $C_2$ se transforma en otra circunferencia $C_2'$ tangente a las rectas paralelas $C_1'$ y $t$. Entonces, la recta $C'$ paralela a $t$ que pasa por $O$ es ortogonal a todas las circunferencias $C_2'$. Tras invertir de nuevo (deshacemos la inversión), $C'$ se transforma en la circunferencia $C$ tangente a $t$ en $B$ y de radio $2r_1$, y es ortogonal a todas las circunferencias $C_2$.

Solución. Como la circunferencia inscrita es tangente al lado $CA$ en $F$, el radio $IF$ es perpendicular a $CA$, luego el triángulo $AFI$ (sombreado en azul) es rectángulo. El segmento $FM$ es una de sus alturas, con lo que $FMI$ es semejante a $AFI$ y esto nos da la relación $\frac{AF}{AM}=\frac{AI}{AF}$, luego $AF^2=AI\cdot AM$. Ahora bien, por la potencia respecto de la circunferencia inscrita, se tiene también que $AF^2=AP\cdot AD$ y, por tanto, $AP\cdot AD=AI\cdot AM$. Usando el recíproco de la propiedad de la potencia (del punto $A$), esto nos dice que $P,I,M,D$ están sobre la misma circunferencia (siempre que no estén alineados).

Nota. Los puntos están alineados cuando la bisectriz del ángulo $A$ pasa por el punto $D$, lo cual es equivalente a que el triángulo $ABC$ sea isósceles (con ángulo desigual en $A$).