Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas

Nota. Los puntos están alineados cuando la bisectriz del ángulo $A$ pasa por el punto $D$, lo cual es equivalente a que el triángulo $ABC$ sea isósceles (con ángulo desigual en $A$).
Informar de error en enunciado Informar de procedencia del problema
Vamos a comenzar demostrando que $P$ está también en esa circunferencia probando que $\angle OPM=180-\angle OBM=180-\frac{\beta}{2}$, donde $\alpha,\beta,\gamma$ denotan los ángulos del triángulo $ABC$. Para probar esto, haremos una caza de ángulos. Como la suma de los ángulos de $ANO$ es $180^\circ$, se tiene fácilmente que $\angle NOA=90-\frac{\alpha}{2}$, de donde se sigue que $\angle NOP=90+\frac{\alpha}{2}$ por ser el ángulo suplementario. Por otro lado, el cuadrilátero $CNOM$ es una cometa (ya que $\angle CNO=\angle CMO$ y $ON=OM$ es el radio de la circunferencia inscrita) luego sus diagonales son perpendiculares, de donde se deduce rápidamente que $\angle ONM=\angle OMN=\frac{\gamma}{2}$. Con todo esto, en el triángulo $ONP$ tenemos que $\angle ONP=\frac{\gamma}{2}$ y $\angle NOP=90+\frac{\alpha}{2}$, luego debe ser $\angle NPO=90-\frac{\alpha+\gamma}{2}=\frac{\beta}{2}$. De aquí que $\angle OPM=180-\frac{\beta}{2}=180-\angle OBM$. Por la propiedad del arco capaz, tenemos que $OPMB$ es un cuadrilátero cíclico.
Esto demuestra que $\angle APB$ es un ángulo recto y un razonamiento similar al anterior demuestra que $\angle AQB$ es también recto, luego $P$ y $Q$ pertenecen a la circunferencia de diámetro $AB$ (en verde en la figura). Ahora bien, en el párrafo anterior también hemos demostrado que $NOP$ tiene ángulos $\angle ONM=\frac{\gamma}{2}$ y $\angle NPO=\frac{\beta}{2}$, luego es semejante a $COB$. Con esta semejanza, llegamos a que \[\frac{BC}{OB}=\frac{NP}{OP}=\frac{NP\cdot OA}{OQ\cdot OB}\ \Leftrightarrow\ MP\cdot OA=BC\cdot OQ,\] donde hemos usado que $OP\cdot OA=OQ\cdot OB$ por la potencia de $O$ respecto de la circunferencia circunscrita a $ANPB$.

Informar de error en enunciado Informar de procedencia del problema
Nota. La cota $\frac{1}{16}$ parece no ser óptima.
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
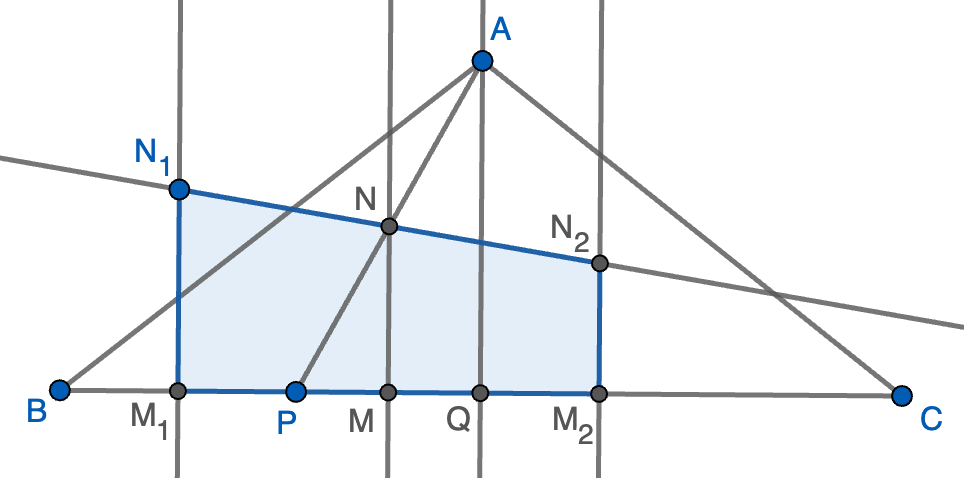
Informar de error en enunciado Informar de procedencia del problema