Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 636
Sea $ABC$ un triángulo acutángulo, $D$, $E$ y $F$ los pies de las alturas que pasan por $A$, $B$ y $C$, respectivamente. Sea $\Gamma$ la circunferencia de diámetro $AD$, que corta a los lados $AB$ y $AC$ en los puntos $X$ e $Y$, respectivamente. Si $P$ es la intersección de $XY$ con $AD$ y $Q$ la intersección de $AD$ y $EF$, demuestra que $P$ es el punto medio de $QD$.
pistasolución 1info
Pista. Demuestra que $XY$ es paralela a $EF$ y corta a $FD$ en su punto medio.
Solución. Sea $H$ el ortocentro del triángulo $ABC$. Como los ángulos $\angle AFH$ y $\angle AEH$ son rectos, tenemos que $AEFH$ es cíclico con diámetro $AH$ (circunferencia verde en la figura). Si hacemos la homotecia con centro en $A$ que lleva $H$ en $D$, esta circunferencia se transforma en $\Gamma$ ya que $AD$ es un diámetro de $\Gamma$. Esto nos dice que $F$ se transforma en $X$ y $E$ en $Y$, así como que $EF$ es paralela a $XY$, $XD$ es paralela a $CF$ y $DY$ paralela a $BE$. Trazamos la paralela a $AB$ que pasa por $D$ (en naranja en la figura), que corta a $CF$ en cierto punto $Z$. Por el paralelismo mencionado y porque $CF$ es la altura perpendicular a $AB$, obtenemos que $XDZF$ es un rectángulo. Ahora bien, usando el arco capaz en $\Gamma$, tenemos que
\[\angle FXY=\angle ADY=90-\angle DAC=\angle ACB.\] De forma similar, usando el arco capaz en la circunferencia circunscrita a $BDHF$ (que también es cíclico), tenemos que
\[\angle XFD=\angle BFD = \angle BHD=90-\angle EBC=\angle ACB.\]
Esto asegura que $XY$ es la diagonal del rectángulo $XDZF$ y, por tanto, corta a la otra diagonal $FD$ en su punto medio $M$. En otras palabras, el vértice $Z$ está sobre $XY$, cosa que no sabíamos inicialmente.
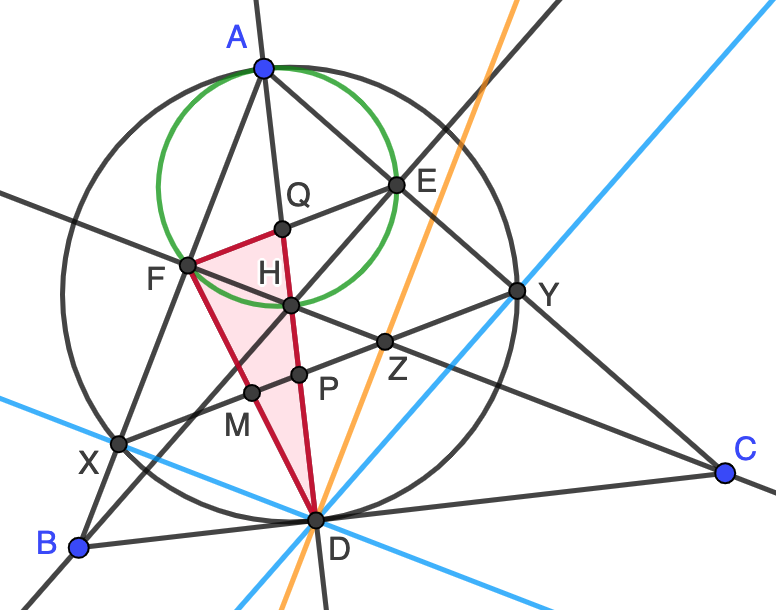
Finalmente, en el triángulo $FDQ$ (sombreado en rojo en la figura) la recta $XY$ es paralela al lado $FQ$ y pasa por el punto medio de $FD$, luego corta a $QD$ también en su punto medio, que es el punto $P$, y el problema está resuelto.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 629
OIM, 2023-P5
Una sucesión $P_1,P_2,\ldots,P_n$ de puntos en el plano (no necesariamente distintos) es carioca si existe una permutación $a_1,a_2,\ldots,a_n$ de los números $1,2,\ldots,n$ para la que los segmentos
\[P_{a_1}P_{a_2},\quad P_{a_2}P_{a_3}, \ldots\quad P_{a_n}P_{a_1}\]
son todos de la misma longitud.
Determinar el mayor número $k$ tal que para cualquier sucesión de $k$ puntos en el plano, se pueden añadir $2023-k$ puntos de modo que la sucesión de $2023$ puntos es carioca.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 628
OIM, 2023-P4
Sean $B$ y $C$ dos puntos fijos en el plano. Para cada punto $A$ del plano que no pertenece a la recta $BC$, sea $G$ el baricentro del triángulo $ABC$. Hallar el lugar geométrico de los puntos $A$ tales que $\angle BAC + \angle BGC = 180^\circ$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 623
OIM, 2022-P5
Sea $ABC$ un triángulo acutángulo con circunferencia circunscrita $\Gamma$. Sean $P$ y $Q$ puntos en el semiplano definido por $BC$ que contiene a $A$, tales que $BP$ y $CQ$ son tangentes a $\Gamma$ con $PB = BC = CQ$. Sean $K$ y $L$ puntos distintos de $A$ en la bisectriz externa del ángulo $\angle CAB$, tales que $BK = BA$ y $CL = CA$. Sea $M$ el punto de corte de las rectas $PK$ y $QL$. Demostrar que $MK = ML$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 619
OIM, 2022-P1
Sea $ABC$ un triángulo equilátero con circuncentro $O$ y circunferencia circunscrita $\Gamma$. Sea $D$ un punto en el arco menor $BC$, con $DB\gt DC$. La mediatriz de $OD$ corta a $\Gamma$ en $E$ y $F$, estando $E$ en el arco menor $BC$. Sea $P$ el punto de corte de $BE$ y $CF$. Demostrar que $PD$ es perpendicular a $BC$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre