Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 596
Sea $P$ un punto del lado $BC$ de un triángulo $ABC$. La paralela por $P$ a $AB$ corta al lado $AC$ en el punto $Q$ y la paralela por $P$ a $AC$ corta al lado $AB$ en el punto $R$. Si la razón entre las áreas de los triángulos $RBP$ y $QPC$ es $k^2$, hallar la razón entre las áreas de los triángulos $ARQ$ y $ABC$.
pistasolución 1info
Pista. Observa que los triángulos $BRP$, $PQC$ y $BAC$ son semejantes y que $ARPQ$ es un paralelogramo.
Solución. Por el paralelismo entre las rectas dadas, está claro que los triángulos $RBP$, $QPC$ y $ABC$ son semejantes ya que tienen sus tres ángulos iguales. También por tener sus lados opuestos paralelos, es fácil darse cuenta de que $ARPQ$ es un paralelogramo, luego $QRQ$ y $PQR$ son triángulos congruentes. Para pasar de $QPC$ a $RBP$ multiplicamos por un factor $k$ (de forma que las áreas se multiplican por $k^2$), luego $BP=k\cdot CP$. De esta forma $BC=(1+k)CP$, luego para pasar de $QPC$ a $ABC$ se multiplica por un factor $1+k$ (y las áreas se multiplican por $(1+k)^2$). Todo esto nos dice que
\begin{align*}
(1+k)^2\mathrm{Área}(RBP)&=\mathrm{Área}(ABC)=\mathrm{Área}(RBP)+\mathrm{Área}(QPC)+2\mathrm{Área}(ARQ)\\
&=\mathrm{Área}(RBP)+k^2\,\mathrm{Área}(RBP)+2\mathrm{Área}(ARQ),
\end{align*}
de donde se tiene que $\mathrm{Área}(ARQ)=k\,\mathrm{Área}(RBP)$. Con esto podemos calcular finalmente
\begin{align*}
\frac{\mathrm{Área}(ARQ)}{\mathrm{Área}(ABC)}=\frac{k\,\mathrm{Área}(RBP)}{(1+k)^2\,\mathrm{Área}(RBP)}=\frac{k}{(1+k)^2}.
\end{align*}
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 594
Demuestra que la longitud de los catetos de un triángulo rectángulo isósceles es siempre igual a la suma de los radios de sus circunferencias inscrita y circunscrita.
pistasolución 1info
Pista. Expresa los radios inscrito y circunscrito en función de las longitudes de los lados del triángulo.
Solución. Pongamos que la hipotenusa del triángulo mide $a$ y los catetos $b$. En un triángulo rectángulo la circunferencia circunscrita tiene a la hipotenusa por diámetro, luego el radio de la circunferencia circunscrita es $R=\frac{a}{2}$. Por otro lado, el área del triángulo es $S=\frac{b^2}{2}$, pero también puede calcularse como $S=pr$, donde $r$ es el radio de la circunferencia inscrita y $p=\frac{1}{2}(a+2b)$ el semiperímetro. Podemos despejar entonces $r=\frac{b^2}{2p}=\frac{b^2}{a+2b}$. Usando el teorema de Pitágoras podemos finalmente calcular
\begin{align*}
R+r&=\frac{a}{2}+\frac{b^2}{a+2b}=\frac{a^2+2ab+2b^2}{2a+4b}\\
&=\frac{4b^2+2ab}{2a+4b}=b.
\end{align*}
Nota. Un cálculo similar muestra que si el triángulo rectángulo no es necesariamente isósceles, entonces $R+r=\frac{b+c}{2}$, donde $b$ y $c$ son las longitudes de los catetos.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 593
Dado un triángulo $ABC$ con baricentro G.
- Demostrar que, para cualquier punto $M$ del plano, se verifica que \[MA^2+MB^2+MC^2\geq GA^2+GB^2+GC^2,\] obteniéndose la igualdad si y solamente si $M = G$.
- Fijado un número $k\gt GA^2+GB^2+GC^2$, hallar el lugar geométrico de los puntos $M$ del plano que cumplen \[MA^2+MB^2+MC^2=k.\]
pistasolución 1info
Pista. Usa coordenadas escribiendo $M$ como un punto arbitrario $(x,y)$ y ahora expresa la cantidad $MA^2+MB^2+MC^2$ en función de $x$ e $y$.
Solución. Vamos a escribir el problema con geometría analítica, de forma que los vértices tienen coordenadas $A=(x_A,y_A)$, $B=(x_B,y_B)$ y $C=(x_C,y_C)$ y consideramos el punto variable $M=(x,y)$. Tenemos entonces que el baricentro tiene coordenadas $G=(\frac{x_A+x_B+x_C}{3}, \tfrac{y_A+y_B+y_C}{3})$, luego podemos calcular
\begin{align*}MA^2+MB^2+MC^2&=(x-x_A)^2+(y-y_A)^2+(x-x_B)^2+(y-y_B)^2+(x-x_C)^2+(y-y_C)^2\\
&=3x^2+3y^2-6x_Gx-6y_Gy+x_A^2+x_B^2+x_C^2+y_A^2+y_B^2+y_C^2\\
&=3\left((x-x_G)^2+\left(y-y_G\right)^2\right)+x_A^2+x_B^2+x_C^2+y_A^2+y_B^2+y_C^2-3x_G^2-3y_G^2
\end{align*}
Sustituyendo $x=x_G$ e $y=y_G$ en la igualdad anterior, obtenemos directamente que
\[GA^2+GB^2+GC^2=x_A^2+x_B^2+x_C^2+y_A^2+y_B^2+y_C^2-3x_G^2-3y_G^2,\]
por lo que se tiene que
\[MA^2+MB^2+MC^2=3MG^2+GA^2+GB^2+GC^2.\]
De aquí se deduce que la desigualdad en el apartado (a) y que la igualdad se alcanza si y sólo si $MG=0$, es decir, cuando $M=G$. Más aún, si $MA^2+MB^2+MC^2=k\gt GA^2+GB^2+GC^2$, entonces la igualdad anterior nos dice que $MG$ es una constante positiva. Deducimos así que los puntos que cumplen (b) son los de una circunferencia centrada en $G$ de radio $\frac{1}{\sqrt{3}}\sqrt{k-GA^2-GB^2-GC^2}$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 590
Sean $ABC$ y $XYZ$ dos triángulos cuyos lados no son paralelos. En ambos triángulos los vértices $A, B, C$ y $X, Y, Z$ están etiquetados en el orden de las agujas
del reloj. Si se cumple que
\[\frac{AB}{XY} = \frac{BC}{YZ} = \frac{CA}{ZX}\quad \text{y} \quad AX = BY = CZ,\]
demostrar que $ABC$ y $XYZ$ tienen el mismo circuncentro.
pistasolución 1info
Pista. Piensa en que $ABC$ y $XYZ$ son semejantes, luego existe un punto $O$ tal que $XYZ$ puede obtenerse mediante una homotecia de $ABC$ de centro $O$ y luego una rotación también de centro $O$ ($O$ es el conocido como centro de semejanza).
Solución. La primera condición nos está diciendo que $ABC$ y $XYZ$ son triángulos semejantes y además esta semejanza es directa (no invierte la orientación) ya que en ambos triángulos los vértices están etiquetados en el mismo orden. Ahora bien, una semejanza directa se puede descomponer como composición de una homotecia y una rotación, ambas con el mismo centro. Llamaremos $O$ a dicho centro, $\lambda$ a la razón de la homotecia y $\theta$ al ángulo de rotación. Esto nos dice que en el triángulo $OAX$ se cumple que $\angle AOX=\theta$ y $OX=\lambda OA$. Podemos resolver usando el teorema del coseno
\[AX^2=OA^2+(\lambda OA)^2-2\lambda OA^2\cos\theta=OA^2(\lambda^2+1-2\lambda \cos\theta).\]
De la misma forma, tenemos que
\[BY^2=OB^2(\lambda^2+1-2\lambda \cos\theta),\qquad CZ^2=OC^2(\lambda^2+1-2\lambda \cos\theta).\]
Ahora bien, como $-1\leq\cos\theta\leq 1$, tenemos que $\lambda^2+1-2\cos\theta\geq\lambda^2+1-2\lambda=(\lambda-1)^2\geq 0$ y la igualdad se da únicamente cuando $\lambda=1$ y $\theta=0$, pero en tal caso no hay rotación y los triángulos $ABC$ y $XYZ$ tendrían sus lados paralelos en contra de lo que se afirma en el enunciado. Tenemos, por tanto que $\lambda^2+1-2\lambda \cos\theta\neq 0$, luego la igualdad $AX=BY=CZ$ se traduce en $OA=OB=OC$, es decir, el centro de semejanza $O$ es el circuncentro de $ABC$. Como la semejanza lleva la circunferencia circunscrita a $ABC$ en la circunferencia circunscrita a su homólogo $XYZ$, concluimos que $O$ también es el circuncentro de $XYZ$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 585
Sea $ABCD$ un cuadrilátero convexo tal que $AB\gt BC$, $CD = DA$ y $\angle ABD =\angle DBC$. Sea $E$ un punto de la recta $AB$ tal que $\angle DEB = 90^\circ$. Probar que $2AE = AB − BC$.
pistasolución 1info
Pista. Toma una circunferencia de centro $D$ que pasa por $A$ y $C$, así como su intersección con las rectas $AB$ y $BC$.
Solución. Consideremos la circunferencia de centro $D$ que pasa por $A$ y $C$. Como $\angle ABD=\angle DBC$, esta circunferencia cortará tanto a $AB$ como a $BC$ en dos puntos distintos, de forma que $A$ es el más alejado de estos dos puntos en $AB$ y $C$ es el más cercano en $BC$. Sea $C'$ el otro punto en que la circunferencia corta a $AC$, que es simétrico de $C$ respecto de la recta $BD$ por la simetría de la figura. Entonces, se tiene que $AB-BC=AB-BC'=AC'=2AE$, ya que la perpendicular trazada por $D$ a $AB$ (punteada en la figura) es la mediatriz de la cuerda $AC'$.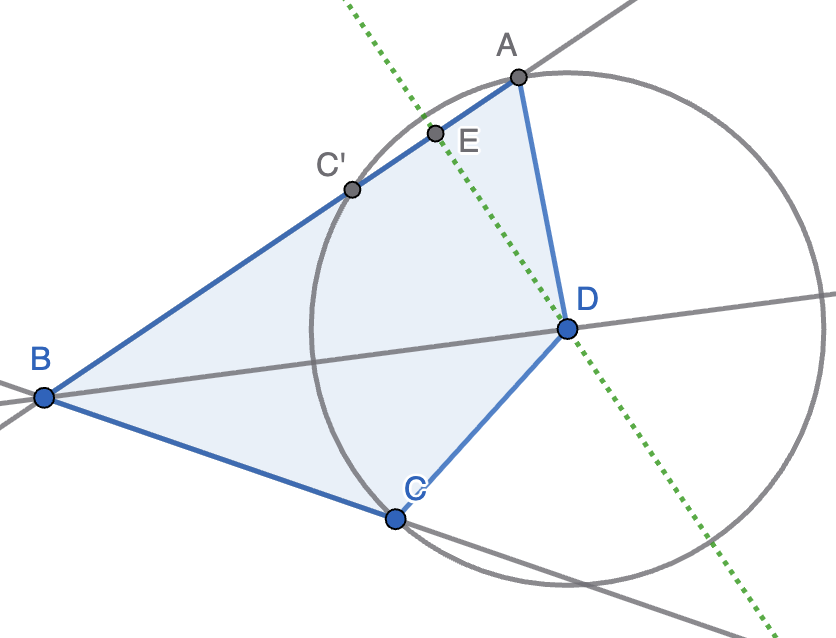

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre