Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Como los triángulos $BFD$ y $BGD$ son rectángulos con hipotenusa común $BD$, deducimos que el cuadrilátero $BFDG$ es cíclico, es decir, hay una circunferencia que pasa por sus cuatro vértice. El centro de dicha circunferencia en $I$, el punto medio del diámetro $BD$. De la misma forma, hay una circunferencia con centro en $J$ en la que se inscribe el cuadrilátero $AECH$. Demostraremos que $KL$ es el eje radical de estas dos circunferencias y, por tanto, ortogonal a la recta $IJ$ que une sus centros.

Para ello, sólo hay que ver que $K$ y $L$ tienen la misma potencia respecto de ambas circunferencias, lo que equivale a decir que $LB\cdot LF=LE\cdot LA$ y $KD\cdot KG=KC\cdot KH$. Sin embargo, la primera igualdad se deduce directamente de que los triángulos $LFA$ y $LEB$ son semejantes, mientras que la segunda viene de que $KGC$ y $KDH$ son semejantes. En ambos casos se trata de triángulos rectángulos con un ángulo (no recto) común.

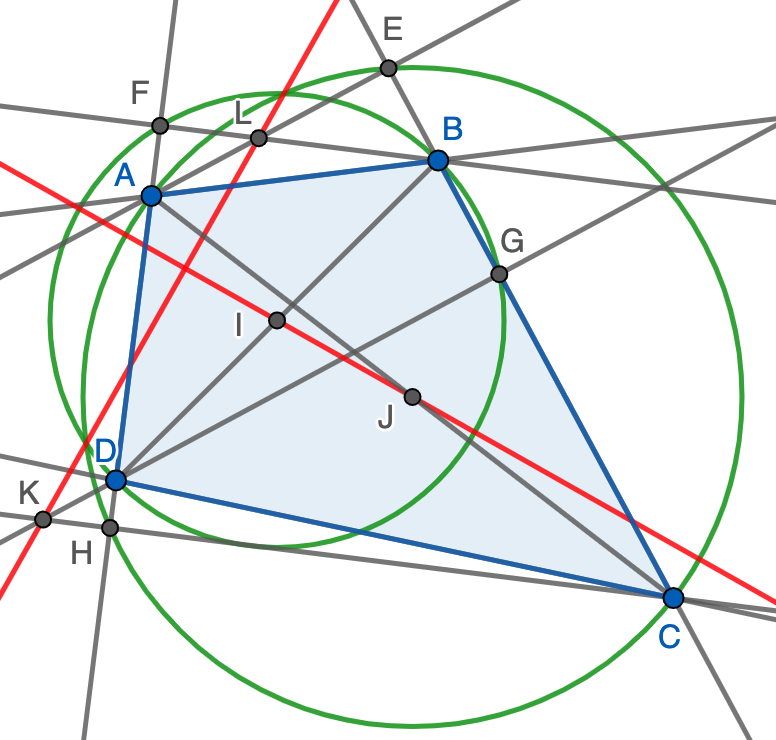
Nota. La demostración vale tanto si el cuadrilátero es cóncavo o convexo, o incluso si no hay cuadrilátero sino solo cuatro puntos dados en el plano. La única salvedad es que $ABCD$ sea un paralelogramo, en cuyo caso $I=J$ (y, por tanto, la recta $IJ$ no está definida) y $K$ y $L$ no existen ya que las rectas cuya intersección los define son paralelas.

Solución. Construimos puntos $P'$ y $Q'$ sobre la recta $PQ$ tales que $PD=P'D$ y $CQ=C'Q$. Supondremos que $P\neq P'$ y $Q\neq Q'$ a menos que $AD$ o $BC$ sean perpendiculares a $PQ$. Observamos que $pp'D$ y $QQ'C$ son isósceles, luego se tiene que $\angle APQ=\angle P'PD=\angle Q'P'D$ y $\angle BQP=\angle Q'QC=\angle P'Q'C$. Esta igualdad de ángulos junto con las proporciones dadas en el enunciado nos dicen que $ABQP$ y $DCQ'P'$ son cuadriláteros semejantes (indicados en rojo y verde en la figura. Por tanto, el ángulo que forman los pares de lados opuestos $AB$ y $PQ$ en $ABQP$ es el mismo que el que forman los lados homólogos $CD$ y $P'Q'$ en $DCQ'P'$. Dicho de otra forma, cuando prolongamos los estos lados, obtenemos triángulos semejantes $APX$ y $DP'Y$ (representados en azul), siendo $X$ la intersección de $PQ$ y $AB$ e $Y$ la intersección de $PQ$ y $CD$. Esto concluye la demostración ya que nos dice que $\angle AXP=\angle DYP$.

Solución. En primer lugar, hay que decir que $P$ no es otra cosa que el baricentro de $ABC$. Como el baricentro dista de un vértice el doble que del punto medio del lado opuesto, tenemos que \[MP=\frac{BM}{3}=\frac{\sqrt{2(a^2+c^2)-b^2}}{6},\quad NP=\frac{CN}{3}=\frac{\sqrt{2(a^2+b^2)-c^2}}{6},\] donde hemos usado la conocida expresión para las medianas del triángulo en términos de las longitudes de los lados. Con esta información, tenemos que el cuadrilátero $ANMP$ tiene una circunferencia inscrita si, y solo si, sus lados opuestos tienen la misma suma. Podemos desarrollar \begin{align*} AM+NP=AN+MP&\Leftrightarrow&\frac{b}{2}+\frac{\sqrt{2(a^2+b^2)-c^2}}{6}=\frac{c}{2}+\frac{\sqrt{2(a^2+c^2)-b^2}}{6}\\ &\Leftrightarrow\ \frac{b}{2}-\frac{c}{2}=\frac{\sqrt{2(a^2+c^2)-b^2}}{6}-\frac{\sqrt{2(a^2+b^2)-c^2}}{6}\\ &\Leftrightarrow\ b-c=\frac{(2(a^2+c^2)-b^2)-(2(a^2+b^2)-c^2)}{3(\sqrt{2(a^2+c^2)-b^2}+\sqrt{2(a^2+b^2)-c^2})}\\ &\Leftrightarrow\ b-c=\frac{c^2-b^2}{\sqrt{2(a^2+c^2)-b^2}+\sqrt{2(a^2+b^2)-c^2}} \end{align*} En los últimos pasos, hemos multiplicado por la expresión conjugada (para eliminar las raíces del numerador) y hemos simplificado. Ahora basta observar que si $b=c$, entonces se tiene la igualdad anterior. Sin embargo, si $b\neq c$, la igualdad no es cierta ya que los dos miembros tienen signos opuestos. Deducimos entonces, que si hay circunferencia inscrita, entonces tiene que ser $b=c$, es decir, el triángulo $ABC$ tiene que ser isósceles.