Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Sumando las tres desigualdades obtenemos que \[360º=\angle APB+\angle BPC+\angle APC\leq 2(\angle ACB+\angle BAC+\angle ABC)=2\cdot 180º=360º,\] por lo que todas las desigualdades del enunciado deben ser igualdades. Ahora bien, estas igualdades son ciertas cuando $P$ coincide con $O$, el circuncentro de $ABC$, usando la propiedad de que ángulo central es el doble del ángulo inscrito. Veamos que si $P\neq O$, entonces alguna de las igualdades no es cierta y esto demostrará que el circuncentro es el único punto que cumple las desigualdades del enunciado.

Consideremos el círculo que pasa por $O$, $A$ y $B$, el círculo que pasa por $O$, $B$ y $C$ y el círculo que pasa por $O$, $A$ y $C$. Si $P\neq O$, entonces $P$ estará en el exterior en uno de estos tres círculos (ya que no tienen puntos interiores común al pasar todos por $O$). Pongamos que $P$ está en el exterior del círculo que pasa por $O$, $A$ y $B$ sin perder generalidad. Las propiedades del arco capaz y del ángulo central nos dicen que $\angle APB\lt \angle AOB=2\angle ACB$, luego no se da la igualdad y hemos terminado.

Nota. Supongamos que $P$ es un punto que se encuentra en el mismo semiplano que $O$ respecto de la recta $AB$. Hemos usado la propiedad de que si $P$ está en el exterior del círculo que pasa por $O$, $A$ y $B$, entonces $\angle APB\lt \angle AOB$. Si, por el contrario, el punto $P$ está en el interior del círculo, entonces $\angle APB\gt \angle AOB$. La igualdad $\angle APB=\angle AOB$ se da únicamente cuando $P$ es parte de la circunferencia.

Solución. Supongamos que el triángulo $ABC$ tiene la recta que une el baricentro $G$ y el incentro $I$ paralela al lado $BC$. Sean $P$, $Q$ y $R$ los pies de las perpendiculares a $BC$ que pasan por $A$, $I$ y $G$, respectivamente. Tenemos así que $IP=r$ es el radio de la circunferencia inscrita y $GR=\frac{1}{3}AP$ ya que los triángulos $APM$ y $GRM$ son semejantes, siendo $M$ el punto medio de $BC$, y el baricentro divide a la mediana $AM$ en los segmentos $AG=2GM$. La condición del enunciado es equivalente a que $r=\frac{1}{3}h$, donde $h=AP$ es la altura sobre lado $BC$.

Ahora bien, el área de $ABC$ se puede calcular como $S=\frac{1}{2}(a+b+c)r$ y también como $S=\frac{1}{2}ah$. Igualando estas dos fórmulas, tenemos que $r=\frac{1}{3}h$ si, y sólo si, $\frac{1}{6}(a+b+c)h=\frac{1}{2}ah$ y esto a su vez equivale a que $b+c=2a$. Obtenemos así que la condición buscada es que la longitud de un lado sea la media aritmética de las longitudes de los otros dos.

Nota. La condición de que el triángulo no sea equilátero es para que el baricéntro y el incentro no sean el mismo punto. ¿Sabrías demostrar por qué?

Solución. Llamemos $a,b,c$ a los lados del triángulo opuestos a los vértices $A,B,C$, respectivamente, y llamemos $h_a$ y $h_b$ a las alturas sobre los lados $a$ y $b$, respectivamente. Como la distancia de $A$ a la recta $BC$ es $h_a$, se tiene que $b\geq h_a\geq a$. Análogamente, como la distancia de $B$ a la recta $AC$ es $h_b$, se tiene que $a\geq h_b\geq b$. Esto nos dice que $a=b$ y también que la distancia de $A$ a la recta $BC$ se realiza en $C$ (es decir, $C$ es el pie de la altura $h_a$). En particular, el ángulo $\angle ACB$ es recto y los ángulos $\angle BAC$ y $\angle ABC$ son de $45º$ por ser $a=b$.

Solución. El cuadrilátero $ABCD$ puede ser o bien un rombo o bien un trapecio isósceles. En el caso del rombo, se tiene que $r_1=r_2=r_3=r_4$ por simetría de la figura, luego la fórmula dada se cumple evidentemente. Supondremos entonces que se trata de un trapecio isósceles y supondremos sin perder generalidad que $BC=AD=1$ y escribiremos $CD=x\lt 1$. La condición de que tiene círculo inscrito nos dice que $AB+CD=BC+AD$, de donde $CD=2-x$.

Los triángulos $BEC$ y $AED$ son congruentes, luego $r_4=r_2$. Los triángulos $AEB$ y $CED$ son semejantes ya que $AB$ y $CD$ son paralelas y están en proporción $2-x$ a $x$. En consecuencia, tenemos que $r_1=\frac{2-x}{x}r_3$, lo que nos permite reescribir la condición del enunciado como: \[\frac{1}{r_1}+\frac{1}{r_3}=\frac{1}{r_2}+\frac{1}{r_4}\ \Leftrightarrow\ r_2=(2-x)r_3.\] Sea $P$ el pie de la perpendicular por $D$ al lado $AB$. El teorema de Pitágoras en el triángulo $APD$ nos dice que $1=AP^2+DP^2=(1-x)^2+DP^2$ y en el triángulo $BDP$ nos dice que $BD^2=DP^2+BP^2=DP^2+1$. De estas dos ecuaciones, se deduce que $DP^2=1+2x-x^2$, luego se tiene por la semejanza entre $CED$ y $AEB$ que \[DE=\frac{x}{2}DP=\frac{x}{2}\sqrt{1+2x-x^2},\qquad BE=\frac{2-x}{2}DP=\frac{2-x}{2}\sqrt{1+2x-x^2}.\] Para obtener la relación entre $r_2$ y $r_3$, usamos que el área de un triángulo es igual al semiperímetro por el radio inscrito en los triángulos $BEC$ y $CED$, que tienen por altura común $h$ a la perpendicular por $C$ a $DB$. En el triángulo $BEC$, tenemos que \[\tfrac{1}{2}(1+\sqrt{1+2x-x^2})r_2=\tfrac{1}{2}BE\cdot h=\frac{2-x}{4}\sqrt{1+2x-x^2}\cdot h,\] mientras que en el triángulo $CED$ obtenemos \[\tfrac{1}{2}(x+x\sqrt{1+2x-x^2})r_3=\tfrac{1}{2}DE\cdot h=\frac{x}{4}\sqrt{1+2x-x^2}\cdot h.\] Despejando e igualando $h$ en ambas fórmulas, se tiene que $r_2=(2-x)r_3$, como queríamos demostrar.

Solución. El área de $H$ se puede escribir como \begin{align*} \mathrm{Area}(H)&=\mathrm{Area}(AB_2C_1)+\mathrm{Area}(AA_1A_2)+\mathrm{Area}(BA_1C_2)\\ &\quad +\mathrm{Area}(BB_1B_2)+\mathrm{Area}(CB_1A_2)+\mathrm{Area}(CC_1C_2)-2\mathrm{Area}(T). \end{align*} Cada uno de los seis triángulos (distintos de $T$) que aparecen en esta expresión son isósceles. Usando que el área de un triángulo es la mitad del producto de dos lados por el seno del ángulo que forman, la suma anterior se puede escribir como \[\mathrm{Area}(H)=\frac{(b+c)^2+a^2}{2}\mathrm{sen}(\alpha)+\frac{(a+c)^2+b^2}{2}\mathrm{sen}(\beta)+\frac{(a+b)^2+c^2}{2}\mathrm{sen}(\gamma)-2\mathrm{Area}(T),\] donde $\alpha,\beta,\gamma$ son los ángulos de $T$ en los vértices $A,B,C$, respectivamente. Si tenemos en cuenta que $\mathrm{Area}(T)=\frac{bc}{2}\sin(\alpha)=\frac{ac}{2}\sin(\beta)=\frac{ab}{2}\sin(\gamma)$, podemos eliminar los senos en la expresión anterior, obteniendo \begin{align*} \mathrm{Area}(H)&=\left(\frac{(b+c)^2+a^2}{bc}+\frac{(a+c)^2+b^2}{ac}+\frac{(a+b)^2+c^2}{ab}-2\right)\mathrm{Area}(T)\\ &=\left(\frac{b^2+c^2+a^2}{bc}+\frac{a^2+c^2+b^2}{ac}+\frac{a^2+b^2+c^2}{ab}+4\right)\mathrm{Area}(T)\\ &=\left((a^2+b^2+c^2)\left(\frac{1}{ac}+\frac{1}{bc}+\frac{1}{ab}\right)+4\right)\mathrm{Area}(T). \end{align*} La desigualdad buscada se deduce entonces de la siguiente \[\frac{a^2+b^2+c^2}{3}\geq\frac{bc+ac+ab}{3}\geq\frac{3}{\frac{1}{ac}+\frac{1}{bc}+\frac{1}{ab}},\] donde hemos usado en primer lugar la desigualdad de reordenación y después la desigualdad entre las medias aritmética y armónica.

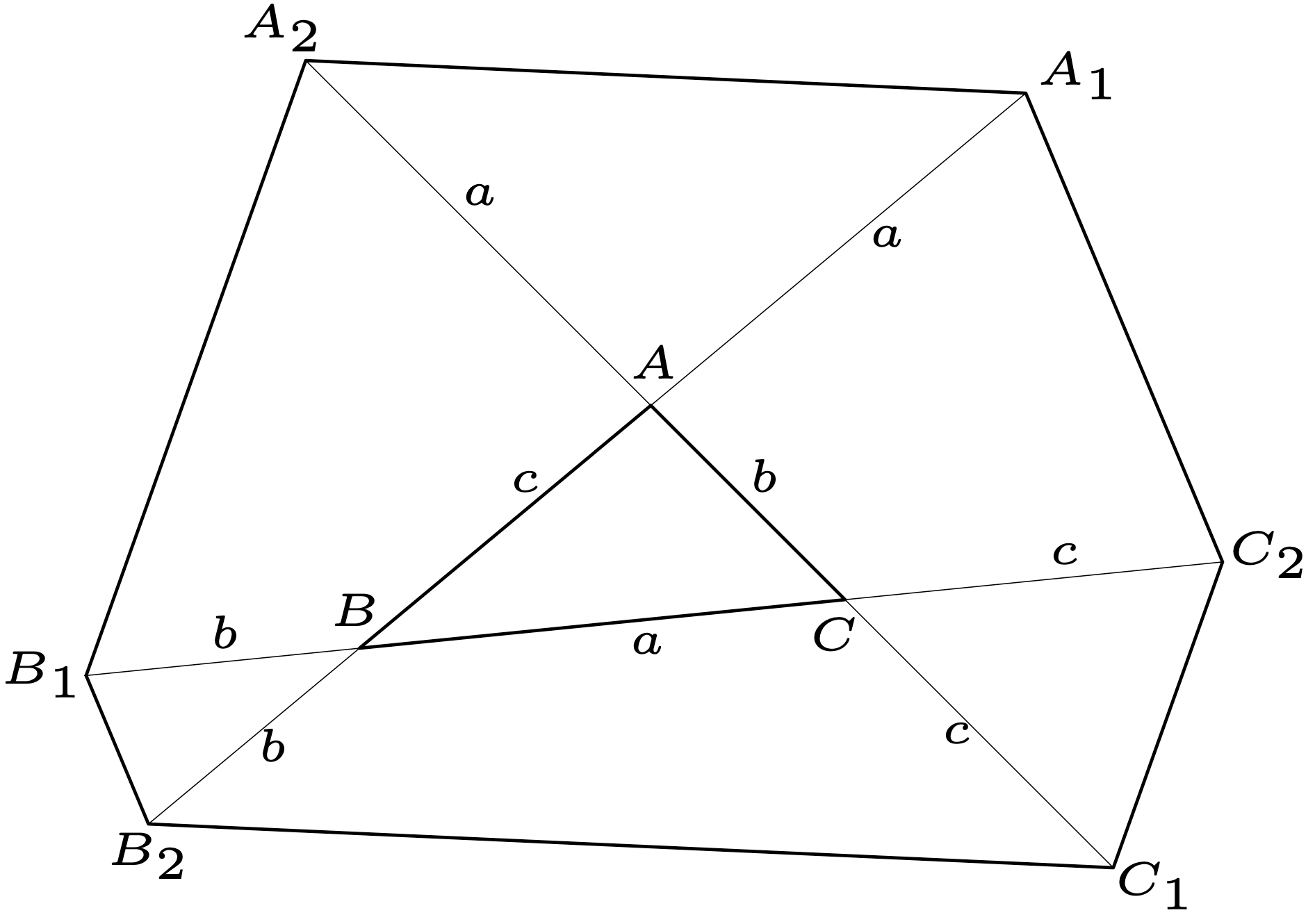
Nota. La igualdad se alcanza si, y sólo si, el triángulo es equilátero.