Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Comenzaremos demostrando que si el triángulo $ABC$ es el de mayor perímetro, entonces $P$ es el incentro. Para ello, vamos a fijar los vértices $B$ y $C$ y mover el vértice $A$ entre todos los puntos de la circunferencia $\Gamma$ de centro $P$ y radio $r$ ($r$ será igual a $3$, $5$ o $7$). Por tanto, el lado $BC$ queda fijo y la suma de distancias $AB+AC$ será constante en cada elipse de focos $B$ y $C$ (por definición de elipse). Si consideramos todas estas elipses, como se muestra en la figura, existirá un punto $Q$ de $\Gamma$ con $QB+QC$ máximo, que se corresponderá con una elipse $E$ tangente en $Q$ a la circunferencia $\Gamma$, como puede verse en la figura (es decir, la elipse de mayor excentricidad que deja a $\Gamma$ en su interior). Observamos que $PQ$ es perpendicular a $\Gamma$ en $Q$ por tratarse de un radio, luego también es perpendicular a $E$ en $Q$ ya que $E$ y $\Gamma$ son tangentes en este punto. Ahora usamos la propiedad de que los segmentos que unen un punto de una elipse con el foco tienen por bisectriz la perpendicular en el punto (ver la nota). Por tanto, el punto $Q$ de $\Gamma$ que maximiza el perímetro cumple que $P$ está en la bisectriz interior del ángulo $A$. Si el triángulo $ABC$ maximiza el perímetro, entonces $P$ tiene que ser el incentro.

Puede parecer que lo anterior demuestra el enunciado, pero podría ocurrir que no hay ningún triángulo $ABC$ cuyo incentro $I$ dista $3$, $5$ y $7$ de los vértices. De hecho, no hemos usado estos tres números para el razonamiento anterior. Tomemos los puntos $P,Q,R$ de los lados $AB,BC,CA$, respectivamente, tales que $IP=IQ=IR=r$, el radio de la circunferencia inscrita. Como estos radios son perpendiculares a los correspondientes lados, en función de $r$, los $360º$ del ángulo completo en $I$ se pueden calcular como \begin{align*} 360º&=\angle AIQ+\angle AIR+\angle RIB+\angle BIP+\angle PIC+\angle CIQ\\ &=2\arccos(\tfrac{r}{3})+2\arccos(\tfrac{r}{5})+2\arccos(\tfrac{r}{7}). \end{align*} Es fácil ver que si esta ecuación se cumple, entonces se pueden construir los seis triángulos rectángulos en que se divide $ABC$ y al unirlos tenemos el triángulo $ABC$ con distancias $3$, $5$ y $7$ al incentro. Definimos entonces la función $f:[0,3]\to\mathbb{R}$ como \[f(r)=2\arccos(\tfrac{r}{3})+2\arccos(\tfrac{r}{5})+2\arccos(\tfrac{r}{7}).\] Esta función es continua y estrictamente decreciente con $f(0)=540^\circ$ y \[f(3)=2\arccos(\tfrac{3}{5})+2\arccos(\tfrac{3}{7})\lt 2\arccos(0)+2\arccos(0)=360^\circ.\] El teorema de Bolzano nos asegura que hay un valor de $r$ para el que $f(r)=360^\circ$.

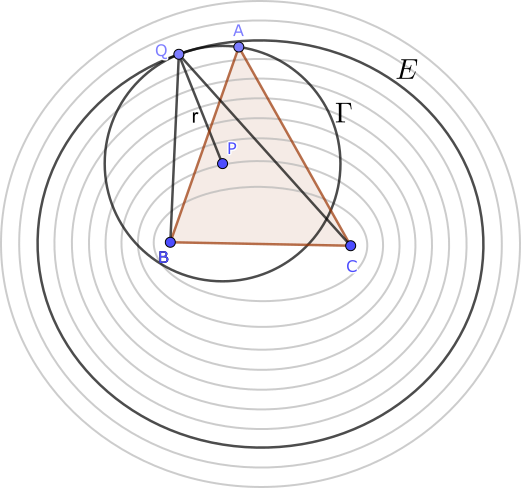
Nota. La propiedad que hemos usado de las elipses es la que hace que, en una sala de planta elíptica, si hablamos en uno de los focos, otra persona oiga con claridad lo que decimos si se sitúa en el otro foco.

Por otro lado, el argumento para la existencia del triángulo no depende realmente de los números $3$, $5$ y $7$ (es decir, se podrían haber escrito otros tres números positivos cualesquiera).

Solución. Sean $M$ el punto medio del lado $BC$ y $P$ el pie de la altura que pasa por $A$ en el lado $BC$. Como $OM$ y $AP$ son paralelas, tenemos que $APD$ es semejante a $OMD$. De esta forma, se cumple que \[\frac{AD-R}{AD}=\frac{OD}{AD}=\frac{OM}{AP}=\frac{OM\cdot BC}{AP\cdot BC}=\frac{\mathrm{Area}(BOC)}{\mathrm{Area}(ABC)},\] donde hemos usado que $OM$ es la alutra del triángulo $BOC$ y la fórmula del área de un triángulo como la mitad de la base por la altura. Repitiendo el mismo argumento para los tres lados del triángulo, se tienen las relaciones \[\frac{AD-R}{AD}=\frac{\mathrm{Area}(BOC)}{\mathrm{Area}(ABC)},\qquad \frac{BE-R}{BE}=\frac{\mathrm{Area}(AOC)}{\mathrm{Area}(ABC)},\qquad \frac{CF-R}{CF}=\frac{\mathrm{Area}(AOB)}{\mathrm{Area}(ABC)}. \] Sumando estas tres igualdades llegamos a que \[3-\frac{R}{AD}-\frac{R}{BE}-\frac{R}{CF}=\frac{\mathrm{Area}(BOC)+\mathrm{Area}(AOC)+\mathrm{Area}(AOB)}{\mathrm{Area}(ABC)}=1,\] de donde se obtiene claramente la fórmula del enunciado.

Solución. Llamemos $\Gamma_1,\Gamma_2,\Gamma_3,\Gamma_4,\Gamma_5$ a las circunferencias y supongamos por hipótesis que existen puntos $p_1,p_2,p_3,p_4,p_5$ tales que $p_i\in\Gamma_j$ siempre que $j\neq i$. Si dos de estos puntos son iguales, entonces hemos terminado (por ejemplo, si $p_1=p_2$, entonces este punto está en las cinco circunferencias puesto que $p_1$ está en todas menos en $\Gamma_1$, pero $p_2$ sí que está en $\Gamma_1$).

Supongamos entonces que los cinco puntos $p_1,p_2,p_3,p_4,p_5$ son distintos. En particular, $p_1,p_2,p_3$ son tres puntos distintos tanto en $\Gamma_4$ como en $\Gamma_5$. Como tres puntos distintos determinan una única circunferencia, deducimos que $\Gamma_4=\Gamma_5$, luego $p_5$ está también en $\Gamma_5$ y, por tanto, es un punto común a todas las circunferencias.

Solución. Si prolongamos los lados del hexágono, se formarán dos triángulos equiláteros (que contienen al hexágono) ya que sus ángulos interiores son iguales y, por tanto, iguales a $120º$ (ver figura). Si llamamos $a,b,c,d,e,f$ a las longitudes de los lados del hexágono (etiquetados de forma consecutiva), el hecho de que tales triángulos sean equiláteros se traduce en que sus lados son iguales, es decir: \begin{align*} a+b+c=c+d+e=e+f+a,\\ b+c+d=d+e+f=f+a+b. \end{align*} Para llegar a estas igualdades, también hemos usado que al prolongar los lados $a$ y $c$ se forma otro triángulo equilátero de lado $b$ (y lo mismo ocurre para el resto de lados, como se ve en la figura). De las dos ecuaciones anteriores, se llega fácilmente a que \[f-c=b-e=d-a.\] Estas diferencias se pueden suponer positivas, si tomamos $f=6$ como el mayor de los lados en nuestro etiquetado. Como $a,b,c,d,e,f$ son los números del $1$ al $6$ en cierto orden, las diferencias anteriores sólo pueden ser iguales a $1$ y $3$. Además, tras aplicar una simetría axial, podemos suponer que $b$ es mayor que $d$, lo que nos da dos posibles casos:

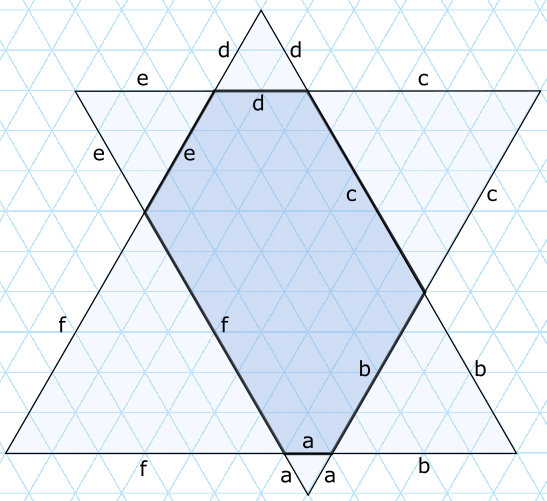
• [Diferencia 3]: $(a,b,c,d,e,f)=(1,5,3,4,2,6)$. El área del hexágono es el área de un triángulo equilátero de lado $a+b+f=12$ menos la suma de las áreas de tres triángulos equiláteros de lados $b=5$, $d=4$ y $f=6$. Como el área de un triángulo equilátero de lado $\ell$ es $\frac{\sqrt{3}}{4}\ell^2$, tenemos que el área del hexágono es \[A=\frac{\sqrt{3}}{4}(12^2-5^2-4^2-6^2)=\frac{67\sqrt{3}}{4}.\]
• [Diferencia 1]: $(a,b,c,d,e,f)=(1,4,5,2,3,6)$. Razonando de forma análoga y teniendo en cuenta que $a+b+f=11$, $b=4$, $d=2$ y $f=6$, llegamos a que \[A=\frac{\sqrt{3}}{4}(11^2-4^2-2^2-6^2)=\frac{65\sqrt{3}}{4}.\]

En la figura, hemos dibujado el segundo de estos dos hexágonos con la ayuda de una malla triangular (el primero se haría de forma similar). Estos son, por tanto, los dos únicos posibles valores del área.

Solución. Sean $P$, $Q$ y $R$ los pies de las alturas de $ABC$ sobre los lados $AB$, $AC$ y $BC$, respectivamente y llamemos $\alpha$, $\beta$ y $\gamma$ a los ángulos de $ABC$ por simplicidad. Vamos a suponer en primer lugar que el triángulo es acutángulo (primera figura). Como el cuadrilátero $APHQ$ tiene dos ángulos rectos, deducimos que $\angle PHQ=\pi-\beta$, luego $\angle CHQ=\beta$. Esto nos dice que los triángulos $CHQ$ y $ABQ$ son semejantes, luego tenemos que $\frac{CH}{HQ}=\frac{AB}{BQ}$. Por hipótesis, estamos suponiendo que $AB=CH$, luego $HQ=BQ$. Es inmediato entonces que $BHQ$ es un triángulo rectángulo isósceles, de donde $\angle HBQ=\frac{\pi}{4}$. Contando ángulos en el triángulo $BRC$, llegamos a que $\gamma=\frac{\pi}{4}$, lo que responde a la pregunta del enunciado.

Supongamos ahora que $\alpha=\frac\pi2$ (se razona igualmente para $\beta=\frac\pi2$), en cuyo caso se tiene que $A=H$ y $ABC$ es un triángulo rectángulo isósceles, de donde también tenemos que $\gamma=\frac{\pi}{4}$. Otro caso posible es que $\alpha\gt\frac\pi2$ (análogamente, se razona para $\beta=\frac\pi2$). En tal caso, la demostración del caso acutángulo se adapta a este caso, teniendo en cuenta ahora que $CHQ$ y $ABQ$ son semejantes por un motivo distinto: ambos son triángulos rectángulos y tienen el mismo ángulo en el vértice común $A$ (opuestos por el vértice).

Queda por analizar el caso en que $\gamma\geq\frac\pi2$. El caso $\gamma=\frac\pi2$ es imposible ya que se tendría que $CH=0$, por lo que supondremos $\gamma\gt\frac\pi2$ (segunda figura). En este caso, $CHQ$ y $ABQ$ vuelven a ser semejantes, lo que nos da de nuevo que $\angle HBQ=\frac{\pi}{4}$. En el triángulo $\angle HBR$, tenemos que $\angle HBR=\frac{\pi}{4}$, $\angle HRB=\frac\pi2$ y $\angle BHR=\pi-\gamma$, luego $\gamma=\frac{3\pi}{4}$.

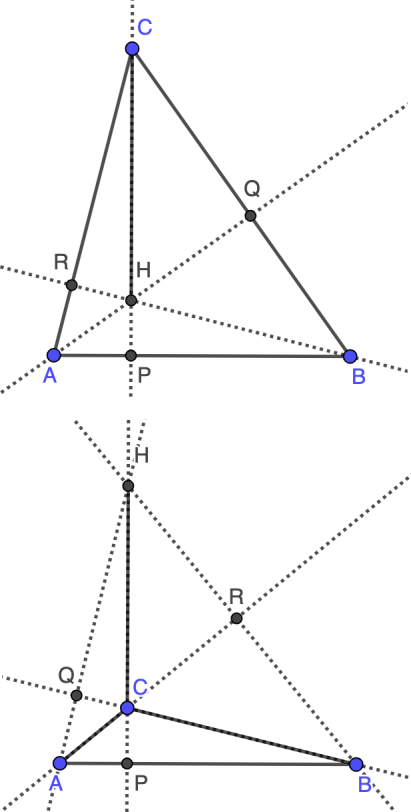
Nota. Este problema es sencillo ya que sólo hay que identificar dos triángulos semejantes en una situación estándar (involucrando al ortocentro). No obstante, se ha marcado con tres estrellas porque es difícil darse cuenta de que puede aparecer una solución distinta si el triángulo es obtusángulo.