Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Para cada $i$ entre $1$ y $n$, consideremos la circunferencia $\Gamma_i$ de centro $P_i$ y radio $|r_i|$. No puede haber dos de los $r_i$ que sean negativos o cero ya que entonces tendríamos una distancia negativa o cero (los puntos deben ser distintos). Distinguimos casos:

• Si todos los $r_i$ son positivos, entonces las circunferencias $\Gamma_1,\ldots,\Gamma_n$ son tangentes exteriores dos a dos. Es bien conocido que el número máximo de circunferencias mutuamente tangentes es cuatro (ver la nota), lo que nos da $n\leq 4$ en este caso.
• Si existe un $r_i$ cero y el resto son positivos, pongamos $r_1=0$, entonces las circunferencias $\Gamma_2,\ldots,\Gamma_n$ son mutuamente tangentes exteriormente y además $P_1$ pertenece a todas ellas. Como los puntos de tangencia de $\Gamma_2,\ldots,\Gamma_n$ son distintos, el punto $P_i$ no puede pertenecer a todas las circunferencias salvo que $n=3$. Esto nos dice que $n\leq 3$ en este caso.
• Si existe un $r_i$ negativo y el resto son positivos, pongamos $r_1\lt 0$, entonces las circunferencias $\Gamma_2,\ldots,\Gamma_n$ son mutuamente tangentes exteriormente, mientras que $\Gamma_1$ es tangente interior a todas las demás (siendo $r_1+r_i\gt 0$, se tiene que $|r_1|\leq |r_i|$ para todo $i$). Esto nos dice que $n\leq 3$ en este caso ya que $\Gamma_1$ no puede ser interior a dos o más circunferencias tangentes exteriormente.

Hemos probado así que el máximo buscado es $n=4$.

Nota. El hecho de que el máximo número de circunferencias mutuamente tangentes es cuatro es consecuencia, por ejemplo, del teorema de los círculos de Descartes (aunque puede razonarse independientemente de forma más elemental).

Solución. Sean $r$ y $s$ las tangentes exteriores a las circunferencias de centros $A$ y $C$ y $r'$ y $s'$ las tangentes exteriores a las circunferencias de centros $B$ y $D$. Una circunferencia tangente a $r$ y $s$ debe equidistar de ambas rectas por lo que su centro pertenece a la bisectriz del ángulo formado por estas (si $r$ y $s$ son paralelas, entonces el centro pertenece a una paralela equidistante a ambas). Esto nos dice que las circunferencias tangentes a $r$ y $s$ tienen su centro en una recta, luego esta debe ser la que contiene a la diagonal $AC$. De la misma forma, debe pertenecer a la diagonal $BD$, luego el centro ha de ser el centro del rectángulo, que denotaremos por $O$.

Consideremos $A'$, $O'$ y $C'$ los pies de las perpendiculares a $r$ que pasan por $A$, $O$ y $C$. Como $AO=OC$, se deduce del teorema de Tales (las rectas $r$ y $AC$ son cortadas por tres paralelas $AA'$, $OO'$ y $CC'$) que $OO'=\frac{1}{2}(AA'+CC')=\frac{1}{2}(a+c)$. Por tanto, la circunferencia con centro $O$ y tangente a $r$ y $s$ tiene radio $\frac{1}{2}(a+c)$. Análogamente, la circunferencia con centro $O$ y tangente a $r'$ y $s'$ tiene radio $\frac{1}{2}(b+d)$. Como $a+c=b+d$, deducimos que ambas son la misma circunferencia y, por tanto, el cuadrilátero que se forma admite una circunferencia inscrita.

Solución. Supongamos que el cuadrado tiene lado 1 sin perder generalidad. Sea $O$ el centro de la circunferencia y sean $M$ y $N$ los puntos medios de los lados $BC$ y $CD$. Llamando $P$ al punto medio de $MN$ y usando el teorema de Pitágoras se calcula fácilmente $AM=\frac{\sqrt{5}}{2}$ y $MP=\frac{1}{2}MN=\frac{\sqrt{2}}{4}$. Además, $AO=OM=R$, el radio de la circunferencia. Por lo tanto, el teorema de Pitágoras en los triángulos rectángulos $AMP$ y $OMP$ nos dice que \[\frac{5}{4}=\frac{1}{8}+(R+OP)^2,\qquad R^2=OP^2+\frac{1}{8}.\] Este sistema de dos ecuaciones con incógnitas $OP$ y $R$ se resuelve fácilmente, obteniendo como únicas soluciones positivas: \[OP=\frac{\sqrt{2}}{3},\qquad R=\frac{5\sqrt{2}}{12}.\] Por lo tanto, la longitud de la circunferencia es $2\pi R=\frac{5\sqrt{2}\pi}{6}$, mientras que el perímetro del cuadrado es $4$. Como $\pi^2\lt 10\lt \frac{576}{50}$, tomando raíces cuadradas obtenemos que $\frac{5\sqrt{2}\pi}{6}\lt 4$, es decir, la longitud de la circunferencia es menor que el perímetro del cuadrado.

Nota. El valor de $R$ también se deduce de la fórmula para el radio de la circunferencia circunscrita al triángulo $AMN$, es decir, \[R=\frac{MN\cdot AM\cdot AN}{\sqrt{p(p-MN)(p-AM)(p-AN)}},\] donde $p=\frac{1}{2}(AM+MN+AN)$ es el semiperímetro del triángulo.

Solución. Consideremos un giro de centro en $C$ y ángulo $60º$ que transforma $ABC$ en otro triángulo equilátero $A'B'C'$ con $B'=A$ y $C'=C$. Llamemos $P'$ al punto en el que se transforma $P$ por dicho giro. Entonces, está claro que $PP'C$ es es equilátero (ya que $PC=P'C$ y $\angle PCP'=60ª$) y $APP'$ tiene por lados $AP$, $AP'=BP$ y $PP'=CP$. Además, se cumple que \[\text{área}(APP')+\text{área}(CPP')=\text{área}(AP'C)+\text{área}(APC)=\text{área}(BPC)+\text{área}(APC).\] Si llamamos $\Delta_a$ a un triángulo equilátero de lado $a$ y $T$ al triángulo de lados $5$, $7$ y $8$, tenemos que \[\text{área}(\Delta_8)+\text{área}(T)=\text{área}(BPC)+\text{área}(APC).\] Análogamente, haciendo giros de $60º$ respecto de los vértices $A$ y $B$, tenemos que \begin{eqnarray*} \text{área}(\Delta_7)+\text{área}(T)&=\text{área}(APB)+\text{área}(BPC),\\ \text{área}(\Delta_5)+\text{área}(T)&=\text{área}(APB)+\text{área}(APC). \end{eqnarray*} Sumando las tres igualdades y teniendo en cuenta que las áreas de los tres triángulos $APB$, $BPC$ y $APC$ suman el área de $\Delta_\ell$, siendo $\ell$ el lado del triángulo $ABC$, llegamos a la identidad \[\text{área}(\Delta_5)+\text{área}(\Delta_7)+\text{área}(\Delta_8)+3\cdot\text{área}(T)=2\cdot\text{área}(\Delta_\ell).\] Usando que $\text{área}(\Delta_a)=\frac{\sqrt{3}}{4}a^2$ y que la fórmula de Herón nos dice que $\text{área}(T)=\sqrt{p(p-5)(p-7)(p-8)}=10\sqrt{3}$, siendo $p=10$ el semiperímetro de $T$, podemos transformar la identidad anterior en la ecuación \[(5^2+7^2+8^2)\frac{\sqrt{3}}{4}+30\sqrt{3}=\frac{\sqrt{3}}{2}\ell^2,\] de donde deducimos que $\ell=\sqrt{129}$.

Solución. Vamos a introducir coordenadas para resolver el problema. Para simplificar los cálculos, tomemos el origen de coordenadas en el vértice $C$ y el eje de abscisas sobre el lado $BC$, de forma que los tres vértices tengan coordenadas \[A=\left(\frac{\ell}{2},\frac{\sqrt{3}}{2}\ell\right),\qquad B=(\ell,0),\qquad C=(0,0),\] siendo $\ell$ el lado del triángulo equilátero $ABC$. Si tomamos $P=(x,y)$, las condiciones dadas en el enunciado pueden reescribirse como \begin{eqnarray*} d(A,P)=5&\Leftrightarrow&\left(x-\frac{\ell}{2}\right)^2+\left(y-\frac{\sqrt{3}}{2}\ell\right)^2=25,\\ d(B,P)=7&\Leftrightarrow&(x-\ell^2)+y^2=49,\\ d(C,P)=8&\Leftrightarrow&x^2+y^2=64.\\ \end{eqnarray*} Usando la tercera ecuación para eliminar los cuadrados de $x$ en $y$ en las dos primeras, podemos despejar $x$ e $y$ en función de $\ell$ como \[x=\frac{\ell^2+15}{2\ell},\qquad y=\frac{\ell^2+63}{2\sqrt{3}\ell}.\] Imponiendo finalmente que $x^2+y^2=64$, obtenemos la ecuación \[\left(\frac{\ell^2+15}{2\ell}\right)^2+\left(\frac{\ell^2+63}{2\sqrt{3}\ell}\right)^2=64\ \Leftrightarrow\ \ell^4-138\ell^2+1161=0.\] Esta ecuación bicuadrada tiene como soluciones positivas $\ell=\sqrt{129}$ y $\ell=3$, aunque ésta última debe descartarse ya que el punto $P$ ha de ser interior al triángulo.

Solución. Si hacemos una inversión respecto de uno de los cinco puntos, éste se va a infinito y los otros cuatro se quedan en el plano. Llamémoslos $A$, $B$, $C$ y $D$ y observemos que los separadores (dependiendo de si contienen o no el centro de inversión) se corresponden con:

• Rectas que pasan por dos de los puntos $A,B,C,D$ y dejan a los otros dos puntos en semiplanos distintos.
• Circunferencias que pasan por tres de los puntos $A,B,C,D$ y dejan al cuarto en su interior.

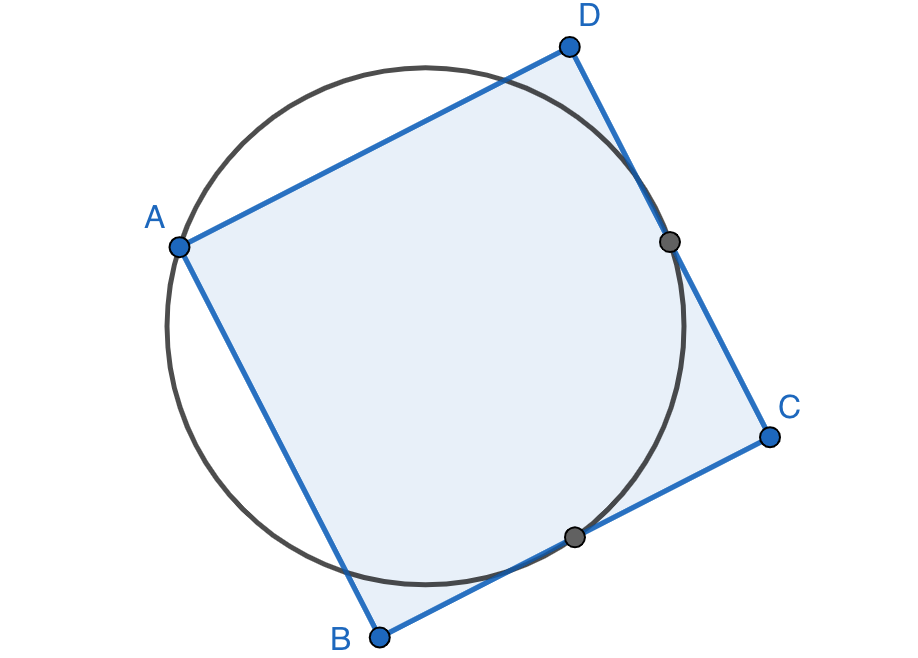
Por consiguiente, tendremos dos posibilidades. La primera de ellas es que los puntos $A,B,C,D$ sean los vértices de un cuadrilátero convexo $ABCD$ (podemos suponer que los vértices están en este orden renombrándolos si es necesario). En tal caso hay dos rectas que pasan por dos de ellos y dejan a los otros dos en semiplanos distintos (las diagonales $AC$ y $BD$) y dos circunferencias que pasan por tres de ellos y dejan al cuarto en su interior (una de las circunferencias circunscritas a $ABC$ ó $ACD$ y una de las circunferencias circunscritas a $BCD$ ó $ABD$). Por tanto, encontramos los cuatro separadores buscados.

La segunda posibilidad es que $ABC$ forme un triángulo y $D$ esté en su interior (después de renombrar los vértices si es necesario). En tal caso, hay tres rectas que pasan por dos de los puntos y dejan a los otros dos en semiplanos distintos ($AD$, $BD$ y $CD$) y una sola circunferencia que pasa por tres de ellos y deja al cuarto en su interior (la circunscrita al triángulo $ABC$). En consecuencia, también hay sólo cuatro separadores en este segundo caso.