Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 342
Consideremos un pentágono en el que cada una de sus diagonales es paralela a uno de sus lados. Demostrar que la razón entre la longitud de una diagonal y la longitud del correspondiente lado paralelo es la misma para cada diagonal.
pistasolución 1info
Pista. Traza las diagonales y busca paralelogramos y triángulos semejantes.
Solución. Denotemos los vértices del pentágono por $A_1,A_2,A_3,A_4,A_5$ en orden cíclico, sus lados opuestos por $\ell_1,\ell_2,\ell_3,\ell_4,\ell_5$ y las diagonales paralelas a estos lados por $d_1,d_2,d_3,d_4,d_5$, respectivamente. Sea $P$ el punto de intersección de las diagonales $d_4$ y $d_1$. Observemos que los triángulos $A_1A_2P$ y $A_3A_5A_2$ son semejantes ya que tienen sus lados paralelos y el cuadrilátero $A_2A_3A_4P$ es un paralelogramo ya que tiene lados opuestos paralelos, de donde $A_2P=\ell_1$. Por tanto, la semejanza de triángulos nos dice que
\[\frac{A_1A_2}{A_3A_5}=\frac{A_2P}{A_5A_2}\ \Longleftrightarrow\ \frac{\ell_4}{d_4}=\frac{\ell_1}{d_1}.\]
Repitiendo el mismo argumento con los otros vértices obtenemos que que $\frac{\ell_1}{d_1}=\frac{\ell_2}{d_2}=\frac{\ell_3}{d_3}=\frac{\ell_4}{d_4}=\frac{\ell_5}{d_5}$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 332
Sea $ABCD$ un cuadrilátero que admite circunferencia circunscrita. Demostrar que
\[|AB-CD|+|AD-BC|\geq2|AC-BD|.\]
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 329
Sea $P$ un punto interior de un triángulo acutángulo $ABC$. Desde el punto $P$ se trazan perpendiculares a los lados $BC$, $AC$ y $AB$, que cortan a éstos en los puntos $A_1$, $B_1$ y $C_1$, respectivamente. ¿Para qué puntos $P$ se cumple que el perímetro del triángulo $A_1B_1C_1$ es mayor o igual que cualquiera de los perímetros de los triángulos $AB_1C_1$, $A_1BC_1$ y $A_1B_1C$?
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 325
Sean $ABC$ un triángulo y $P$ un punto en su interior. Consideremos $P_1$ y $P_2$ los pies de las perpendiculares por $P$ a los lados $AC$ y $BC$, respectivamente, y sean $Q_1$ y $Q_2$ los pies de las perpendiculares desde $C$ a las rectas $AP$ y $BP$. Demostrar que las rectas $AB$, $P_1Q_2$ y $P_2Q_1$ son concurrentes.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 321
Dado un pentágono regular, construir un triángulo que tenga la misma área.
pistasolución 1info
Pista. Moviendo los vértices del pentágono a lo largo de ciertas rectas, el área no cambia.
Solución. Llamemos $ABCDE$ al pentágono y tracemos por $D$ una paralela a $CE$ y por $B$ una paralela a $AC$. Estas paralelas cortan a la recta que contiene a $AE$ en $D'$ y $B'$, respectivamente, como se muestra en la figura. Entonces, los triángulos $CDE$ y $CD'E$ tienen la misma área, así como los triángulos $ABC$ y $AB'C$. Por tanto, el área del pentágono $ABCDE$ es igual al área del triángulo $B'CD'$.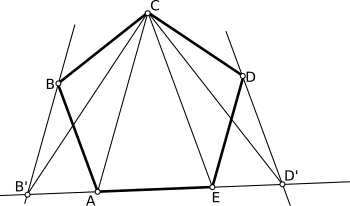

Nota. ¿Cuáles son los ángulos del triángulo construido? ¿Es equilátero?
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre