Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 2767
APMO, 2000-P4
Sean $n$ y $k$ enteros positivos tales que $n\gt k$. Demostrar que
\[\frac{1}{n+1}\cdot\frac{n^n}{k^k(n-k)^{n-k}}\lt\frac{n!}{k!(n-k)!}\lt\frac{n^n}{k^k(n-k)^{n-k}}.\]
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 2733
Sean $a,b,c\in(0,\frac{\pi}{2})$ las raíces de las ecuaciones
\[\cos(x)=x,\qquad \mathrm{sen}(\cos(x))=x,\qquad \cos(\mathrm{sen}(x))=x,\]
respectivamente. Ordenar de menor a mayor los tres números $a,b,c$, justificando la respuesta.
pistasolución 1info
Pista. Utiliza que $\operatorname{sen}(x)\lt x$ para todo $x\in(0,\frac{\pi}{2})$.
Solución. Como $\operatorname{sen}(x)\lt x$ para todo $x\in(0,\frac{\pi}{2})$ y el coseno es una función decreciente, tenemos la cadena de desigualdades
\[\operatorname{sen}(\cos(x))\lt\cos(x)\lt\cos(\operatorname{sen}(x)).\]
Por tanto, los puntos en que estas funciones cortan a la recta $y=x$ estarán en el mismo orden que las funciones, es decir, $b\lt a\lt c$ (en la imagen puede verse una representación gráfica de las tres funciones y la recta).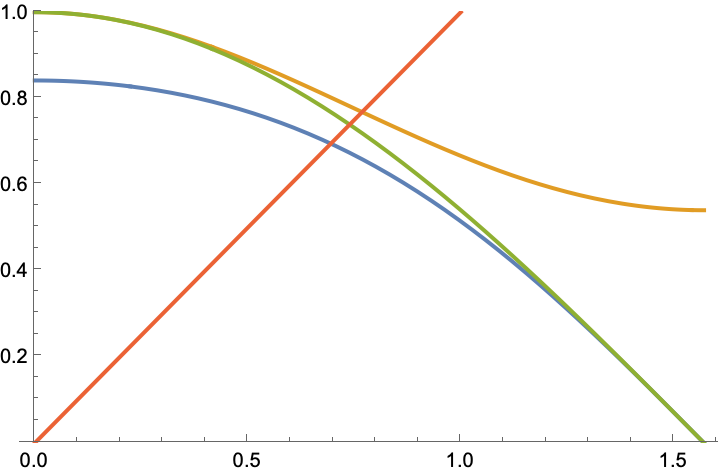

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 2726
Si $a,b,c$ son números reales positivos, demostrar que
\[a^2+b^2+c^2-ab-bc-ca\geq 3(b-c)(a-b).\]
¿Cuándo se verifica la igualdad?
pistasolución 1info
Pista. Pasa todo al miembro de la izquierda y factoriza.
Solución. Si pasamos todo al miembro de la izquierda y operamos, llegamos a la desigualdad equivalente $a^2-4ab+4b^2+2ac-4bc+c^2\geq 0$, que no es otra cosa que
\[(a-2b+c)^2\geq 0.\]
Escrita de esta forma la desigualdad es evidente ya que cualquier número al cuadrado es mayor o igual que cero. Además, la igualdad se cumple si y sólo si $a-2b+c=0$, es decir, si $b$ es la media aritmética de $a$ y $c$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 2714
USAMO, 1998-P5
Sean $a_1, a_2, \dots, a_n$ números enteros positivos tales que
\[\sum_{i=1}^{n} \frac{1}{a_i} \geq 1.\]
Demostrar que
\[\sum_{i=1}^{n} \frac{1}{a_i + 1} \geq \frac{1}{2}.\]
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 2712
USAMO, 1998-P3
Sean $a_0, a_1, \dots, a_n$ números del intervalo $(0, \pi/2)$ tales que
\[\tan\left(a_0 - \frac{\pi}{4}\right) + \tan\left(a_1 - \frac{\pi}{4}\right) + \dots + \tan\left(a_n - \frac{\pi}{4}\right) \geq n - 1.\]
Demostrar que
\[\tan a_0 \cdot \tan a_1 \cdot \dots \cdot \tan a_n \geq n^{n+1}.\]
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre