Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2434 problemas y 940 soluciones.
Problema 1420
Representar gráficamente la función
\[y=\Bigl|\bigl||x-1|-2\bigr|-3\Bigr|\]
en el intervalo $-8\leq x\leq 8$.
pistasolución 1info
Pista. Restar un número positivo consiste en desplazar la gráfica hacia abajo y tomar el valor absoluto es reflejar respecto del eje OX la parte negativa de la función.
Solución. Sólo hay que observar que restar un número equivale a desplazar verticalmente la gráfica y tomar el valor absoluto es reflejar la parte que está en el semiplano inferior respecto del eje OX. De esta forma, empezando con la función identidad $y=x$ hay que seguir los siguientes pasos: bajarla 1 unidad, reflejar, bajarla 2 unidades, reflejar, bajarla 3 unidades y reflejar. Indicamos en la figura el resultado final y algunos pasos intermedios: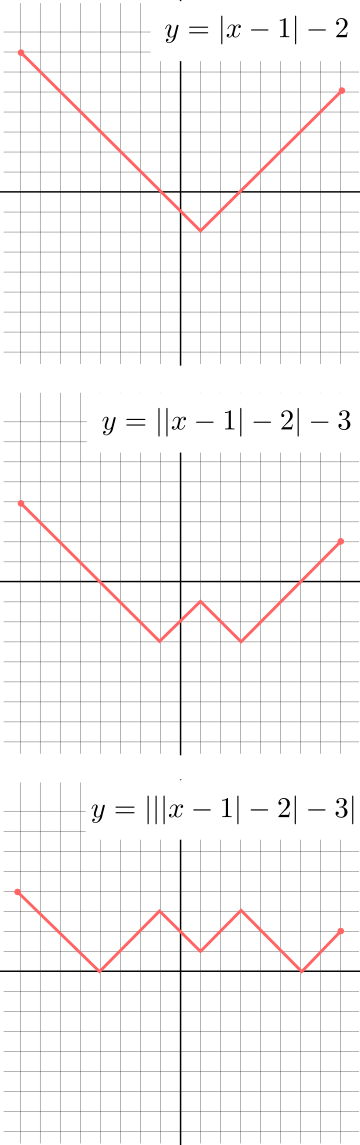

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1417problema obsoleto
El impuesto sobre el Rendimiento del Trabajo Personal es una función $f(x)$ del total $x$ de las retribuciones anuales (en pesetas), de la que se conocen las siguientes propiedades:
- $f(x)$ es una función continua.
- La derivada $f'(x)$ en el intervalo $0\leq x\lt 60000$ es constante e igual a cero; en el intervalo $60000\lt x\lt P$ es constante e igual a $1$; y para $x\gt P$ es constante e igual a $0.14$.
- $f(0)=0$ y $f(140000) = 14000$.
pistasolución 1info
Pista. Observa que $f(x)$ es constante $0$ en $0\leq x\leq 60000$, es de la forma $x+a$ para $60000\leq x\leq P$ y de la forma $0.14x+b$ para $x\geq P$. Ajusta las constantes $a$ y $b$ usando la continuidad.
Solución. Como la derivada es cero para $0\leq x\lt 60000$ y $f(0)=0$, se deduce que $f(x)=0$ para $0\leq x\leq 60000$. En el intervalo $60000\lt x\lt P$, la derivada es constante $1$, luego la función es de la forma $f(x)=x+a$ para cierto número real $a$. Imponiendo por continuidad que $f(60000)=0$, llegamos a que $a=-60000$. Finalmente, como $f'(x)=0.14$ para $x\geq P$, tendrá que ser $f(x)=0.14x+b$ para todo $x\geq P$ y para cierta constante $b$. Para que esto concuerde por continuidad con el intervalo anterior, tenemos que
\[f(P)=P-60000=0.14P+b,\]
luego debe ser $b=0.84P-60000$. En resumidas cuentas, hemos probado que
\[f(x)=\begin{cases}0&\text{si }0\leq x\lt 60000,\\
x-60000&\text{si }60000\leq x\leq P,\\
0.14x+0.86P-60000&\text{si }x\geq P.\end{cases}\]
Ahora bien, como $f(140000)=14000\neq 140000-60000$, no puede ser $140000\leq P$, luego ha de ser $140000\gt P$ y se aplica la tercera línea de la definición de $f(x)$, es decir,
\[14000=f(140000)=0.14\cdot 140000+0.84 P-60000.\]
Esta ecuación de primer grado tiene solución $P=\frac{2720000}{43}\approx 63255.8$.
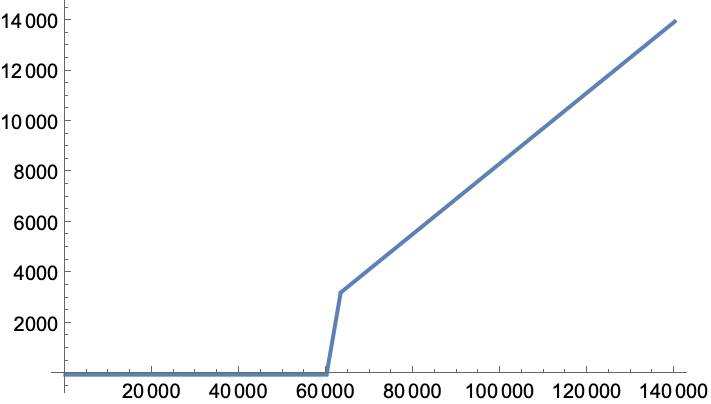
Para representar la gráfica de la función, solo hay que darse cuenta de que está formada por tres trozos rectilíneos: el primero es la constante cero, el segundo tiene pendiente $1$ que pasa por el punto $(60000,0)$ y el tercero tiene pendiente $0.14$ y pasa por $(140000,14000)$. Queda así una gráfica como se muestra en la figura.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1416problema obsoleto
Consideremos la ecuación $x^2+ax+1=0$.
- Determinar el intervalo en que debe mantenerse el número real $a$ para que las raíces de la ecuación sean imaginarias.
- Hallar el lugar geométrico de los puntos representativos de esas raíces en el plano complejo cuando $a$ recorre dicho intervalo.
pistasolución 1info
Pista. Encuentra una relación sencilla entre las partes real e imaginaria de dichas soluciones.
Solución. Las soluciones de esta ecuación de segundo grado son
\[z=\frac{-a\pm\sqrt{a^2-4}}{2}.\]
El radicando es negativo precisamente cuando $-2\lt a\lt 2$, lo que nos da la respuesta al apartado (a). Para responder al apartado (b), escribimos $z=x+iy$, siendo
\[x=\frac{-a}{2},\qquad y=\pm\frac{\sqrt{4-a^2}}{2}=\pm\sqrt{1-x^2}.\]
Deducimos entonces que $x^2+y^2=1$, es decir, los puntos del lugar geométrico están contenidos en la circunferencia de centro $(0,0)$ y radio $1$. Como $x=\frac{-a}{2}$ se mueve en el intervalo $(-1,1)$ y para cada valor de $x$ hay dos valores de $y$ opuestos, deducimos que el lugar geométrico son todos los puntos de esta circunferencia excepto $(1,0)$ y $(-1,0)$. Notemos que estos puntos no podían estar a priori ya que representan números reales.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1415
IMO, 1967-P6
En una competición deportiva hay $m$ medallas que se dan en $n$ días sucesivos, siendo $n\gt 1$. El primer día se da una medalla y $1/7$ de las restantes. El segundo día, se dan dos medallas y $1/7$ de las restantes, y así sucesivamente. El día $n$-ésimo, que es el último, se dan $n$ medallas y no sobra ninguna. ¿Cuántos días duró la competición y cuántas medallas se dieron?
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1414
IMO, 1967-P5
Consideremos la sucesión $\{c_n\}$ definida por
\[c_n=a_1^n+a_2^n+\ldots+a_s^n,\]
en donde $a_1,a_2,\ldots,a_s$ son números reales no todos ellos nulos. Supongamos que hay un número infinito de términos $c_n$ que son iguales a cero. Determinar los valores de $n$ para los que $c_n=0$.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2025. Esta página ha sido creada mediante software libre