Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 1429
Un tronco de cono de revolución tiene su base mayor de radio $r$ y sus generatrices forman con el plano de la base un ángulo cuya tangente vale $m$. Este tronco de cono está formado por un material de densidad $d$ y su base menor está recubierta por una lámina cuya masa es de $p\,$g/cm$^2$ . ¿Cuál es la altura del tronco para la cual la masa total es máxima?
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1427
Es bien sabido que si $\frac{p}{q}=\frac{r}{s}$, entonces ambas razones son iguales a $\frac{p-r}{q-s}$. Escribimos ahora la igualdad
\[\frac{3x-b}{3x-5b}=\frac{3a-4b}{3a-8b}.\]
Por la propiedad anterior, ambas fracciones deben ser iguales a
\[\frac{3x-b-3a+4b}{3x-5b-3a+8b}=\frac{3x-3a+3b}{3x-3a+3b}=1,\]
mientras que las propuestas son de ordinario distintas de la unidad. Explicar con claridad a qué se debe este resultado.
pistasolución 1info
Pista. Se está produciendo una indeterminación $\frac{0}{0}$ en algún momento.
Solución. Tenemos que
\[\frac{3x-b}{3x-5b}=\frac{3a-4b}{3a-8b}\ \Longleftrightarrow\ (3x-b)(3a-8b)=(3a-4b)(3x-5b)\ \Longleftrightarrow\ b(x-a+b)=0.\]
Por lo tanto, con la hipótesis de que ambas razones son iguales, necesariamente $b=0$ (en cuyo caso sí se tiene claramente que ambas son igual a $1$ y no hay paradoja) o bien $x-a+b=0$ (en cuyo caso la última igualdad no es $1$ ya que el denominador es cero y no puede hacerse el razonamiento).
En otras palabras, si $\frac{p}{q}=\frac{r}{s}$ entonces estas razones coinciden con $\frac{p-r}{q-s}$ con la condición adicional de que $q-s$ no sea cero.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1425problema obsoleto
Un disco microsurco gira a velocidad de $33\tfrac{1}{3}$ revoluciones por minuto y su duración es de $24$min $30$s. La parte grabada tiene $29$ cm de diámetro exterior y $11.5$cm de diámetro interior. Con estos datos, calcular la longitud del surco grabado.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1422
En un plano vertical se consideran los puntos $A$ y $B$, situados sobre una recta horizontal, y la semicircunferencia de extremos $A$ y $B$ situada en el semiplano inferior. Un segmento de longitud $a=AB$ se mueve de manera que contiene siempre el punto $A$ y que uno de sus extremos recorre la semicircunferencia dada. Determinar el valor del coseno del ángulo que debe formar ese segmento con la recta horizontal, para que su punto medio esté lo más bajo posible.
Sin pistas
Sin soluciones
infoSi crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
Problema 1420
Representar gráficamente la función
\[y=\Bigl|\bigl||x-1|-2\bigr|-3\Bigr|\]
en el intervalo $-8\leq x\leq 8$.
pistasolución 1info
Pista. Restar un número positivo consiste en desplazar la gráfica hacia abajo y tomar el valor absoluto es reflejar respecto del eje OX la parte negativa de la función.
Solución. Sólo hay que observar que restar un número equivale a desplazar verticalmente la gráfica y tomar el valor absoluto es reflejar la parte que está en el semiplano inferior respecto del eje OX. De esta forma, empezando con la función identidad $y=x$ hay que seguir los siguientes pasos: bajarla 1 unidad, reflejar, bajarla 2 unidades, reflejar, bajarla 3 unidades y reflejar. Indicamos en la figura el resultado final y algunos pasos intermedios: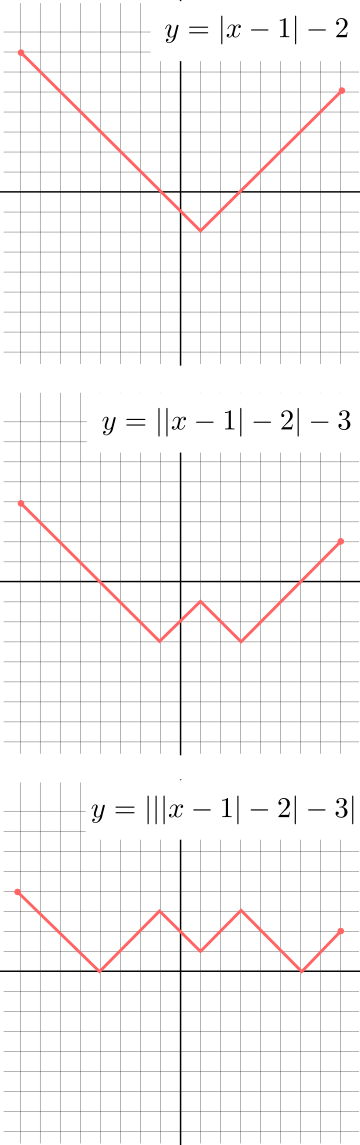

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre