Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 1021
¿Qué valores han de tener los ángulos $\alpha$, $\beta$ y $\gamma$ de un triángulo $T$ para que este se pueda dividir en tres triángulos congruentes entre sí?
pistasolución 1info
Pista. Observa que si para subdividir unimos un vértice con un punto del lado opuesto, entonces necesariamente este segmento tiene que ser perpendicular al lado.
Solución. Hay cuatro formas esencialmente distintas de dividir un triángulo en tres triángulos, que está indicadas en la figura de abajo. Sin embargo, nos damos cuenta de que si un segmento termina en el interior de un lado y no es perpendicular a dicho lado, entonces forma dos ángulos suplementarios distintos. Estos dos ángulos deben ser dos de los ángulos de cada triángulo semejante pero un triángulo no puede tener dos ángulos que sumen $180^\circ$. Esto descarta directamente los casos III y IV y restringe el caso II. Veamos directamente qué restricciones adicionales nos da el hecho de que los tres triángulos deben tener ángulos iguales.
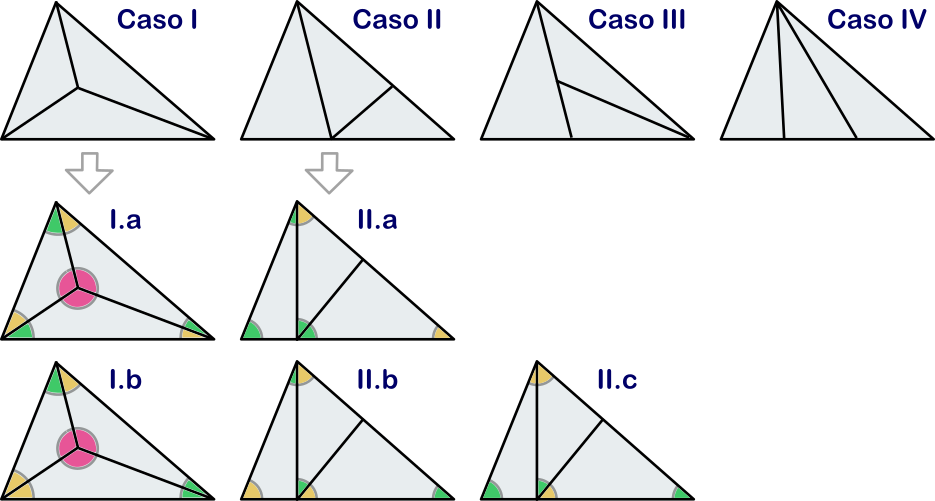
- Caso I. Tenemos un vértice interior, en el que se forman al menos dos ángulos obtusos, que deben ser iguales, y el tercero debe ser igual también ya que suma con uno de los obtusos más de $180^\circ$. Hay dos posibles configuraciones para los otros seis ángulos de los tres triángulos, que hemos llamado casos I.a y I.b. En el caso I.a, como la suma de los ángulos de $T$ es $180^\circ$, llegamos a que el ángulo verde más el amarillo suman $60^\circ$, luego $T$ es equilátero. En el caso I.b, el triángulo $T$ es isósceles, luego los ángulos amarillo y verde deben coincidir y también llegamos a que $T$ es equilátero.
- Caso II. Hay esencialmente tres configuraciones para los ángulos que no son rectos, que se indican en los casos II.a, II.b y II.c. En el caso II.a, dos verdes suman $90^\circ$, de donde se tiene que tanto el verde como el amarillo deben ser $45^\circ$ y $T$ es un triángulo rectángulo isósceles. En el caso II.b, el verde y el amarillo suman $90^\circ$, luego $T$ es en principio un triángulo rectángulo cualquiera. En el caso II.c, tenemos que $T$ es un triángulo isósceles cualquiera.
Tenemos, por tanto, que los únicos triángulos que pueden admitir la subdivisión son los triángulos rectángulos y los triángulos isósceles. Sin embargo, las subdivisiones que nos salen nos dan triángulos congruentes solamente en el caso del triángulo equilátero. Subdividiendo este último uniendo cada vértice con el centro, confirmamos que los triángulos equiláteros son las únicas soluciones.

Nota. Hemos probado, de hecho, que los únicos triángulos que se pueden subdividir en tres triángulos semejantes son los triángulos rectángulos y los triángulos isósceles.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre