Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
Supongamos ahora que uno de los dos números es impar y vamos a ver que es imposible la coloración en este caso. Razonando por reducción al absurdo, nos damos cuenta de que en uno de los lados de longitud impar hay un número impar de lados coloreados de uno de los colores y que este color no aparece más en ningún otro lado del rectángulo $m\times n$. Como el número total de lados pintados de ese color es $mn$, uno por cada pieza cuadrada, y este número es par, debe haber necesariamente una cantidad impar de lados impares pintados en el interior del rectángulo. Esto es una contradicción ya que los lados pintados de un color que son interiores deben estar en número par pues los lados que se pegan deben ser del mismo color.
Falta por comprobar si se puede hacer la coloración cuando tanto $m$ como $n$ son pares. La imagen de la derecha nos muestra un patrón que podemos usar para colorear cualquier rectángulo $m\times 2$ ($m$ par) como nos pide el enunciado y la imagen de la derecha nos muestra un patrón para colorear cualquier rectángulo $m\times 2$ ($m$ par) pero ahora de forma que los lados de la derecha y la izquierda tengan el mismo color. Por lo tanto, adjuntando rectángulos $m\times 2$ del tipo de la izquierda a la derecha del patrón de la derecha, obtenemos coloraciones de cualquier rectángulo $m\times n$ con $m$ y $n$ pares.
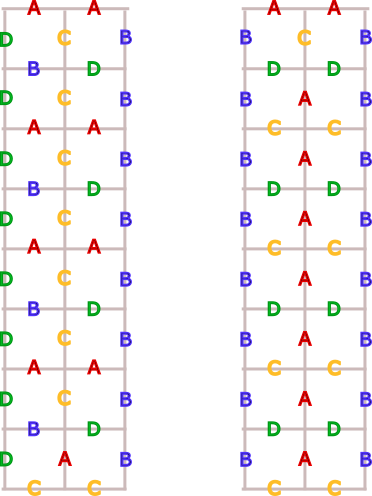
Nota. Este mismo problema apareció en la All-Soviet Union Mathematical Competition de 1984.
Informar de error en enunciado Informar de procedencia del problema