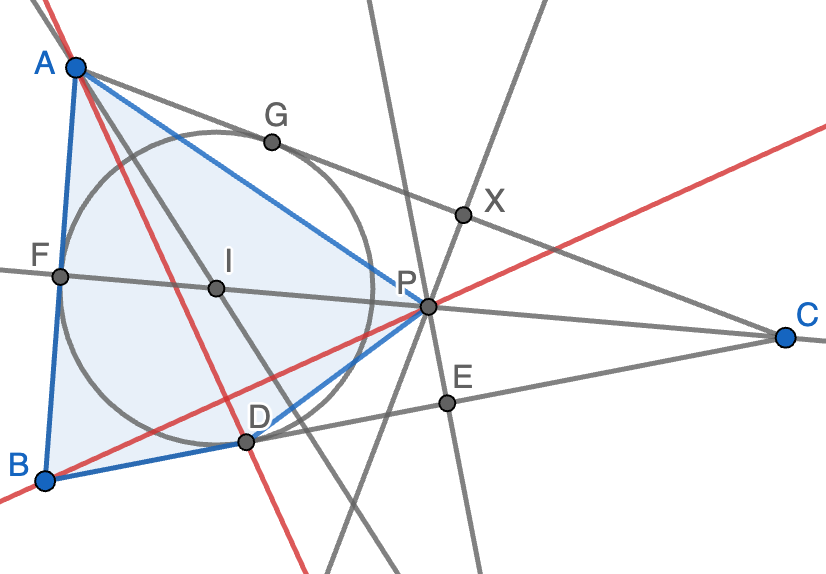
Sea $ABC$ un triángulo con $AB\lt AC$ y sea $I$ su incentro. La circunferencia inscrita en $ABC$ es tangente al lado $BC$ en el punto $D$. Sea $E$ el único punto que satisface que $D$ es el punto medio del segmento $BE$. La línea perpendicular a $BC$ que pasa por $E$ corta a $CI$ en el punto $P$. Demostrar que $BP$ es perpendicular a $AD$.
pistasolución 1solución 2info
Pista. Demuestra que $AB^2+DP^2=AP^2+BD^2$, lo que implica que las diagonales del cuadrilátero $ABDP$ son perpendiculares. Alternativamente, demuestra que la recta $AD$ es el eje radical de las circunferencias centradas en $B$ y $P$ que pasan por $D$.
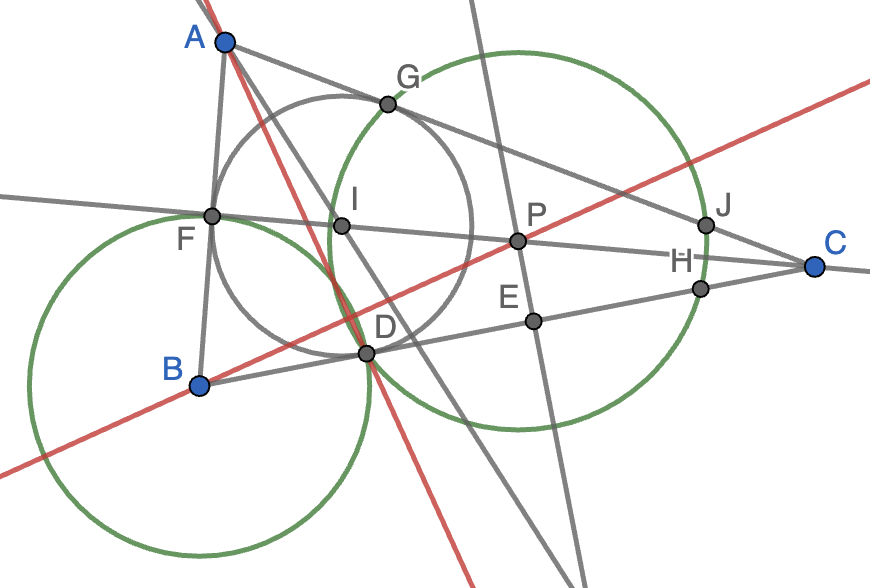
Solución. Sean $F$ y $G$ los puntos en que la circunferencia inscrita es tangente a los lados $AB$ y $AC$, respectivamente. Como $P$ está en la bisectriz $CI$, está a la misma distancia de $G$ y de $D$, luego hay una circunferencia de centro $P$ que pasa por $G$ y $D$, que corta de nuevo a los lados $BC$ y $AC$ en puntos $H$ y $J$, respectivamente, como se muestra en la figura. También está claro que hay una circunferencia de centro $B$ que pasa por $D$ y $F$. Vamos a ver que $AD$ es el eje radical de ambas circunferencias, luego será perpendicular a $BP$, la recta que une sus centros.
Para ver esto, será suficiente ver que $A$ tiene la misma potencia respecto de ambas circunferencias. La potencia de $A$ respecto de la circunferencia de centro $B$ es $AF\cdot(AF+2BF)$. La potencia de $A$ respecto de la circunferencia de centro $P$ es $AG\cdot AJ$. Ahora bien, tenemos que $AG=AF$ por estar $A$ en la bisectriz del ángulo $A$ y $GJ=DH$ por estar $P$ en la bisectriz del ángulo $C$. Además, $DH=2DE$ por ser $E$ el pie de la perpendicular a la cuerda $DH$ desde el centro $P$ y, finalmente, $DE=BD$ por la hipótesis del enunciado. Tenemos así que $AG\cdot AJ=AF\cdot(AF+2BF)$, como queríamos demostrar.
Solución. Vamos a probar que $AB^2+DP^2=AP^2+BD^2$, lo que implica que las dos diagonales del cuadrilátero $ABDP$ (sombreado en azul) son perpendiculares y se tiene el resultado deseado. Sea $X$ el pie de la perpendicular por $P$ al lado $AC$. Usando que $PX=PE$ y $BD=BE$, así como el teorema de Pitágoras en los triángulos rectángulos $AXP$ y $DPE$, tenemos que
\[AB^2+DP^2=AB^2+DE^2+PE^2=AB^2+BD^2+PX^2=BD^2+AP^2+AB^2-AX^2,\]
luego será suficiente con probar que $AB=AX$.
Para ello, sean $F$ y $G$ los puntos en que la circunferencia inscrita es tangente a los lados $AB$ y $AC$, respectivamente. Usando que $CX=CE$, $BF=BD=DE$, $AF=AG$ y $CG=CD$, tenemos que
\[AX=AC-CX=AG+CG-CE=AF+CG-CD-BD+2BD=AF+BF=AB.\]