Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 1109
Los vértices de un triángulo equilátero $ABC$ de lado $1$ están en la superficie de una esfera de radio $1$ y centro $O$. Sea $D$ la proyección ortogonal de $A$ sobre el plano $\alpha$ determinado por $B$, $C$ y $O$. Llamamos $N$ a uno de los cortes con la esfera de la recta perpendicular a $\alpha$ por $O$. Hallar la medida del ángulo $\angle DNO$.
Nota. La proyección ortogonal de $A$ sobre $\alpha$ es el punto de corte con $\alpha$ de la recta perpendicular a $\alpha$ que pasa por $A$.
pistasolución 1info
Pista. Demuestra que $D$ es el centro del triángulo equilátero $OBC$.
Solución. Tenemos que $OA=OB=OC=1$ y $AB=AC=BC=1$, luego $OABC$ es un tetraedro regular y $D$ es el centro de la cara $OBC$, que es un triángulo equilátero. En particular, $OD$ es $\frac{2}{3}$ de la altura de este triángulo, luego $OD=\frac{2}{3}\frac{\sqrt{3}}{2}=\frac{1}{\sqrt{3}}$. Ahora bien, la recta $ON$ es paralela a $DA$ ya que ambas son perpendiculares a $\alpha$, luego los puntos $A,O,N,D$ están todos en un plano perpendicular a $\alpha$. El triángulo $DNO$ es rectángulo y en él puede verse que el ángulo buscado $\angle DNO$ tiene tangente $\frac{OD}{ON}=\frac{1}{\sqrt{3}}$, luego ha de ser $\angle DNO=30^\circ$.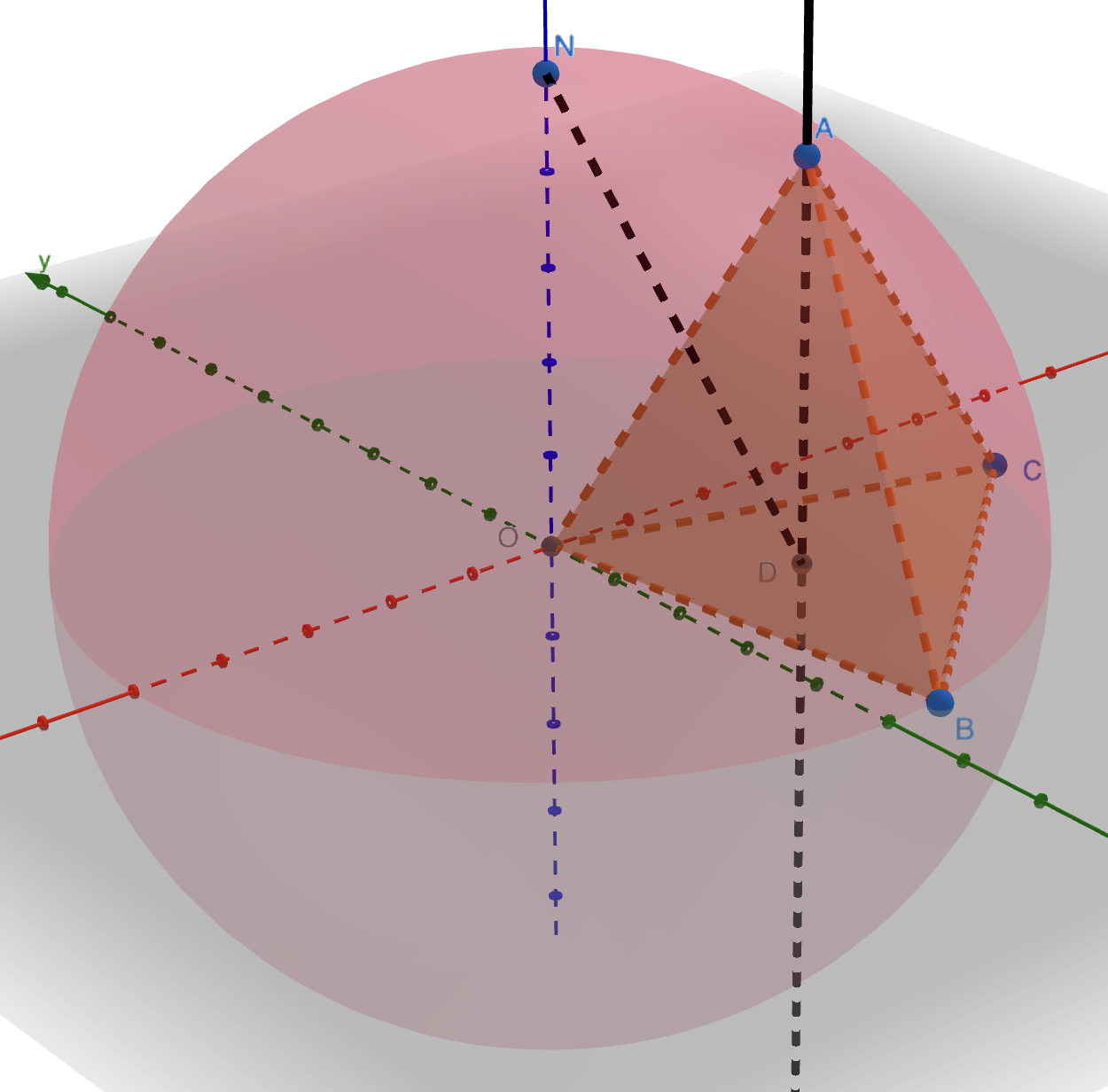

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre