Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
Nota. No se puede expresar el resultado final en términos de funciones trigonométricas.
En el pentágono regular de lado $1$ de la figura, los triángulos $ACD$ y $DEP$ son semejantes pues sus lados son paralelos. Si llamamos $d$ a la longitud de la diagonal del pentágono, la semejanza $\frac{AD}{CD}=\frac{DE}{PE}$ se escribe como $\frac{d}{1}=\frac{1}{d-1}$, de donde $d$ cumple la ecuación $d^2-d-1=0$, de la que nos quedamos con la única solución positiva $d=\frac{1+\sqrt{5}}{2}$, la razón áurea. Ahora bien, el triángulo $ABQ$ de la figura es rectángulo y cumple $\angle BAQ=54$, luego \begin{align*}
\mathrm{sen}(54)&=BD=\frac{d}{2}=\frac{1+\sqrt{5}}{4},\\
\cos(54)&=AQ=\sqrt{1-BQ^2}=\sqrt{1-\left(\tfrac{1+\sqrt{5}}{4}\right)^2}=\frac{\sqrt{5-\sqrt{5}}}{2\sqrt{2}}.
\end{align*}
De esta forma, tenemos que el área del triángulo es
\[8\,\mathrm{sen}(54)\cos(54)=8\frac{1+\sqrt{5}}{4}\cdot\frac{\sqrt{5-\sqrt{5}}}{2\sqrt{2}}=\sqrt{10+2\sqrt{5}}.\]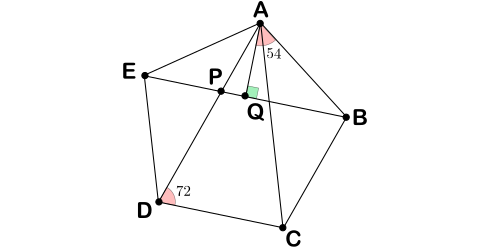
Informar de error en enunciado Informar de procedencia del problema