Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Pintamos de cuatro colores (rojo, amarillo, verde y azul) las esquinas de la mesa y supondremos que partimos de la esquina roja. Ahora usamos el truco de reflejar el cuadrado respecto de sus lados para obtener un tablero infinito, como puede verse en la imagen. De esta forma, la trayectoria de la pelota se convierte en una línea recta sobre la cuadrícula ya que el ángulo de incidencia es el mismo que el de reflexión. El problema se reduce a llegar del punto rojo de la esquina inferior izquierda a otro punto coloreado sin pasar por un punto intermedio y atravesando exactamente 15 lados de la cuadrícula. Si escribimos cada punto con dos coordenadas enteras $(a,b)$, siendo $(0,0)$ la esquina inicial de color rojo, los posibles puntos de destino serán los que cumplen $a+b=17$, que son los 16 puntos sobre la línea de color turquesa en la imagen.

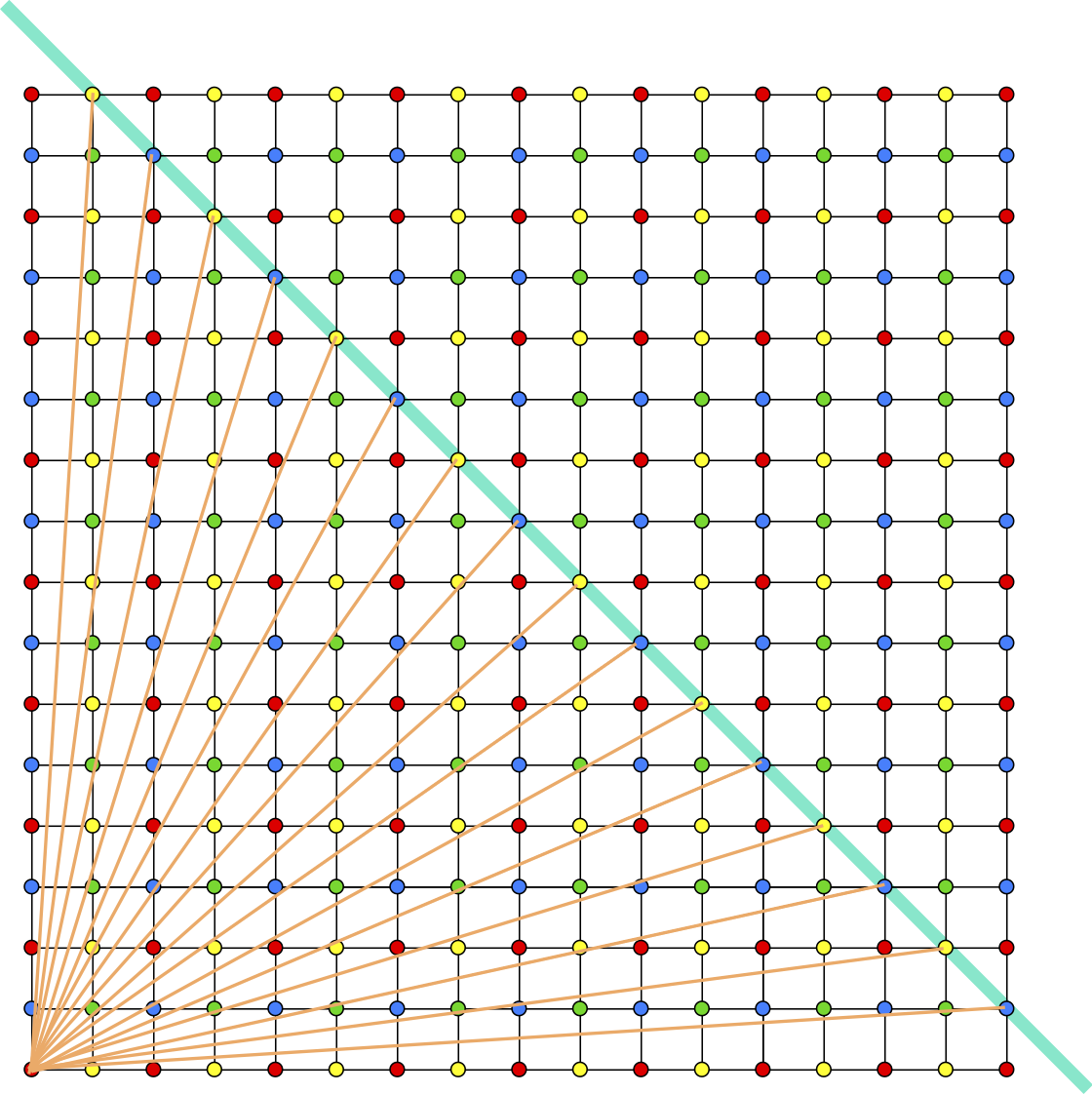
Si unimos $(0,0)$ y $(a,b)$ tal que $a+b=17$, no encontraremos ningún otro punto intermedio en el camino ya que esto supondría encontrar $(c,d)$ proporcional a $(a,b)$, lo que equivale a encontrar un divisor común a $a$ y $b$ (véase la nota). Cualesquiera dos enteros $a,b\geq 1$ tales que $a+b=17$ tienen máximo común divisor $1$ (son primos entre sí) ya que $17$ es primo, luego no existen los mencionados puntos intermedios. En otras palabras, los segmentos dibujados de color naranja no tienen más puntos de coordenadas enteras que sus extremos. Deducimos así que las únicas esquinas que se pueden alcanzar son la de color azul y la de color amarillo, es decir, las adyacentes a la esquina inicial.

Veamos ahora cuál es la longitud mínima, lo que equivale a minimizar $a^2+b^2$ (la distancia al origen al al cuadrado) de entre todos los puntos $(a,b)$ con $a,b\in\mathbb{N}$ y $a+b=17$. A la vista de la figura anterior, está claro que los puntos buscados son $(8,9)$ y $(9,8)$, pero vamos a verlo de forma rigurosa. Completando cuadrados, tenemos que \[a^2+b^2=a^2+(17-a)^2=2a^2-34a+289=2(a-\tfrac{17}{2})^2+\tfrac{289}{2}\] es una parábola con coeficiente cuadrático positivo, luego su mínimo (vértice) se obtiene para $a=\frac{17}{2}$. Los dos valores enteros más cercanos son $a=8$ y $a=9$, que son simétricos respecto del vértice $a=\frac{17}{2}$, luego ambos realizan el mínimo. La distancia mínima es, por tanto, $\sqrt{8^2+9^2}=\sqrt{145}$.

Nota. Si el segmento que une $(0,0)$ y $(a,b)$ contiene otro punto $(c,d)$ de coordenadas enteras, entonces existe $0\lt \lambda\lt 1$ tal que $c=\lambda a$ y $d=\lambda b$, lo que nos dice que $\lambda=\frac{c}{a}=\frac{d}{b}$ es racional. Pongamos $\lambda=\frac{m}{n}$ como fracción irreducible, luego $c=\frac{m}{n}a$ y $d=\frac{m}{n}b$ nos dicen que $n\gt 1$ es un factor común a $a$ y $b$. Recíprocamente, si $n$ es un factor común a $a$ y $b$, entonces $(c,d)=(\frac{a}{n},\frac{b}{n})$ es un punto de coordenadas enteras en el segmento que une $(0,0)$ y $(a,b)$.

Por otro lado, un argumento similar prueba que no se puede alcanzar la esquina opuesta o la inicial tras un número impar de rebotes. Alcanzar la esquina opuesta requeriría un número par de rebotes, mientras que nunca se puede llegar a la esquina inicial pues antes se debería haber pasado por otra esquina, cosa que prohíbe el enunciado.