Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 1136
Se consideran dos rectas paralelas que dividen a un cuadrado de lado $1$ en tres regiones que tienen la misma área. ¿Cuál es la distancia máxima y mínima que puede haber entre ambas rectas?
pistasolución 1info
Pista. Observa en primer lugar la simetría del sistema y que, para cada pendiente, solo hay un par de rectas que cumplan la propiedad. Hay dos casos posibles: que cada recta corte a dos lados opuestos del cuadrado o que corte a dos lados contiguos. Analiza ambos casos por separados y expresa en ambos la distancia como una función de algún parámetro.
Solución. Vamos a suponer por comodidad que el cuadrado tiene sus vértices en el plano con coordenadas $(0,0),(1,0),(1,1),(0,1)$ y vamos a parametrizar los distintos casos usando la pendiente $m$ de las rectas paralelas (observamos que, para cada pendiente, hay un único par de rectas que cumple el requisito de la trisección). Aplicando un movimiento rígido podemos suponer además que $0\leq m\leq 1$. Es interesante darse cuenta de que para $m=\frac{2}{3}$ se tiene una trisección especial (figura central) en la que las rectas pasan por vértices del cuadrado. No es difícil calcular en este caso que la distancia entre las dos rectas es $d=\frac{1}{\sqrt{10}}$. Por la simetría de las regiones respecto de la recta de pendiente $m$ que pasa por el centro $(\frac12,\frac12)$, podemos distinguir dos casos:
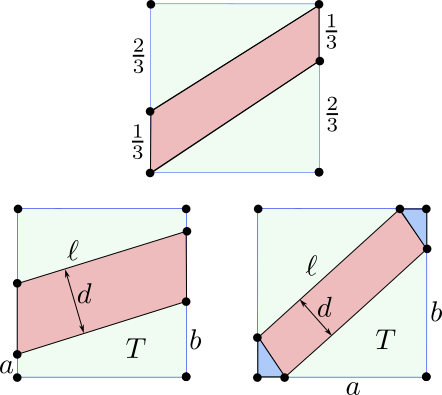
- Caso 1. Las rectas paralelas cortan al cuadrado en lados opuestos. Como la región que delimitan estas rectas es un paralelogramo de base $\ell$ y altura $d$ (según la figura de la izquierda), la condición sobre el área nos dice que $d\cdot\ell=\frac{1}{3}$. Además, si la recta inferior corta a los lados en $(0,a)$ y $(1,b)$ con $b\geq a$, entonces el teorema de Pitágoras nos dice que $\ell^2=1+(b-a)^2$. Además, como el área del trapecio $T$ que queda por debajo de la recta es $\frac{1}{3}$, se tiene que $1\cdot \frac{a+b}{2}=\frac{1}{3}$, o equivalentemente $a+b=\frac{2}{3}$. De todo esto inferimos que \[d=\frac{1}{3\ell}=\frac{1}{3\sqrt{1+(b-a)^2}}=\frac{1}{3\sqrt{1+4(a-\frac{1}{3})^2}}.\] Esto define a $d$ como función de $a$ y además se tiene que $0\leq a\leq\frac{1}{3}$ (si fuera $a\gt\frac{1}{3}$, entonces $b\geq a\geq \frac{1}{3}$ y $T$ contendría un rectángulo de área mayor que $\frac{1}{3}$). En este intervalo la función $1+4(a-\frac{1}{3})^2$ es decreciente, luego $d$ es una función creciente de $a$. El valor mínimo $d=\frac{1}{\sqrt{13}}$ se obtiene para $a=0$ y el máximo $d=\frac{1}{3}$ para $a=\frac{1}{3}$.
- Caso 2. Las rectas paralelas cortan al cuadrado en lados contiguos. Pongamos entonces que la recta inferior corta a los lados en los puntos $(1-a,0)$ y $(0,b)$ con $b\geq a$, lo que define un triángulo $T$ bajo dicha recta. Como el área de $T$ debe ser $\frac{1}{3}$, deducimos que $ab=\frac{2}{3}$. El área de la región entre las dos paralelas está formado por un rectángulo de base $\ell=\sqrt{a^2+b^2}$ y altura $d$ más dos triángulos rectángulos de catetos $1-a$ y $1-b$, lo que nos da un área total $\ell\cdot d+(1-a)(1-b)$. Podemos despejar entonces \begin{align*} d=\frac{\frac{1}{3}-(1-a)(1-b)}{\ell}&=\frac{a+b-\frac{4}{3}}{\sqrt{a^2+b^2}}\\ &=\frac{a+\frac{2}{3a}-\frac{4}{3}}{\sqrt{a^2+\frac{4}{9a^2}}}=\frac{3(a-\frac{2}{3})^2+\frac{2}{3}}{\sqrt{9a^4+4}}. \end{align*} Ahora bien, esto define de nuevo a $d$ como función de $a$ y en este caso $a$ se mueve en el intervalo $[\frac{2}{3},1]$ (si fuera $a\lt \frac{2}{3}$, entonces $T$ estaría contenido en un triángulo de área menor que $\frac{1}{3}$). Para hallar el mínimo de esta función consideramos su derivada, que podemos factorizar como \[d'=\frac{4 \left(9 a^4-9 a^3+6 a-4\right)}{\left(9 a^4+4\right)^{3/2}}=\frac{4(3a^2-2)(3a^2-3a+2)}{\left(9 a^4+4\right)^{3/2}}.\] El factor $3a^2-3a+2$ es siempre positivo y el factor $3a^2-2$ se anula en $a\pm\frac{\sqrt{6}}{3}$. Deducimos que $d$ es decreciente en $[\frac{2}{3},\frac{\sqrt{6}}{3}]$ y creciente en $[\frac{\sqrt{6}}{3},1]$. Por lo tanto, el valor mínimo es $d=\sqrt{2}-\frac{2\sqrt{3}}{3}$, que se obtiene para $a=\frac{\sqrt{6}}{3}$. Para el valor máximo, evaluamos los extremos del intervalo y obtenemos que $d=\frac{1}{\sqrt{13}}$ para $a=\frac{2}{3}$ y también para $a=1$.
Comparando los valores obtenidos, llegamos a que el valor mínimo de la distancia es $\frac{1}{3}$, que se obtiene para dos rectas paralelas a los lados, y que su valor mínimo es $\sqrt{2}-\frac{2\sqrt{3}}{3}$.

Nota. En el problema original, se precisaba no hacer uso de derivadas, lo que requería una dosis de ingenio considerable para cazar el valor $a=\frac{2\sqrt{3}}{3}$ del caso 2. En realidad, la función $d$ en este caso tiene una simetría oculta ya que $d(a)=d(\frac{2}{3a})$. Esto nos asegura que el valor de $a$ tal que $a=\frac{2}{3a}$ debe haber un punto crítico y puede probarse que la función decrece hasta este punto y luego crece. Los detalles puedes encontrarlos en la solución oficial del problema.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre