Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 1143
Decimos que un rectángulo de base $b$ y altura $h$ es áureo si se cumple la proporción
\[\frac{b}{h}=\frac{h}{b-h}.\]
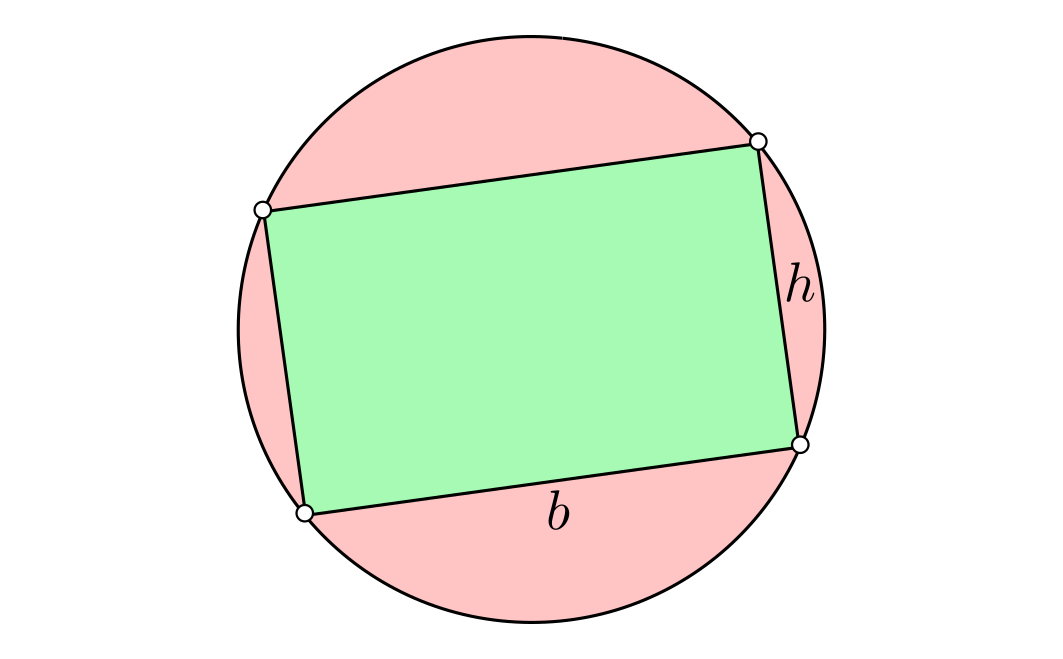
Dado un rectángulo áureo, si trazamos una circunferencia que pase por todos sus vértices, ¿cuál es mayor: el área del rectángulo (representada en verde en la figura) o el área del trozo de círculo que es exterior al rectángulo (representada en rojo)?
pistasolución 1info
Pista. Calcula el área del círculo y del rectángulo en función de $b$ y $h$.
Solución. La condición de rectángulo áureo se puede reescribir como $b^2-bh-h^2=0$. Dividiendo por $h^2$, se tiene la ecuación de segundo grado $(\frac{b}{h})^2-\frac{b}{h}-1=0$ con incógnita $\frac{b}{h}$. Como el cociente de longitudes $\frac{b}{h}$ es positivo, sólo nos interesa la única solución positiva de esta ecuación, dada por
\[\frac{b}{h}=\frac{1+\sqrt{5}}{2}.\qquad(\star)\]
El área del rectángulo (representada en verde en la figura) es $A=bh$. Por otro lado, la circunferencia que pasa por los vértices tiene centro en el centro del rectángulo, luego su radio es la distancia entre dicho centro y uno de los vértices. El teorema de Pitágoras aplicado a un triángulo rectángulo de vértices el centro, un vértice y el punto medio de un lado nos dice que $r^2=(\frac{b}{2})^2+(\frac{h}{2})^2$. Por tanto, el área de la región roja es $A'=\pi r^2-A=\frac{\pi}{4}(b^2+h^2)-bh$. Tendremos que estudiar el signo de la diferencia $A-A'$. A la vista de la igualdad ($\star$), dividimos por $h^2$ y obtenemos
\[\frac{A-A'}{h^2}=\frac{b}{h}-\frac{\pi}{4}\left(\!\left(\frac{b}{h}\right)^{\!2}\!\!+1\!\right)\!+\frac{b}{h}=\frac{1+\sqrt{5}}{2}-\frac{\pi}{4}\left(\!\left(\frac{1+\sqrt{5}}{2}\right)^{\!2}+1\!\right)\approx 0.19.\]
Como este número es mayor que cero y $h^2>0$, deducimos que el área del rectángulo es mayor que la de la región restante del círculo.
Nota. Otra opción para finalizar el ejercicio es darse cuenta de que el siguiente cociente es mayor que $1$: \[\frac{A}{A'}=\frac{\frac{b}{h}}{\frac{\pi}{4}((\frac{b}{h})^2+1)-\frac{b}{h}}=\frac{\frac{1+\sqrt{5}}{2}}{\frac{\pi}{4}((\frac{1+\sqrt{5}}{2})^2+1)-\frac{1+\sqrt{5}}{2}}\approx 1.32,\] donde hemos dividido numerador y denominador por $h^2$ para poder aplicar ($\star$). Una alternativa a esto último es suponer a lo largo de todo el razonamiento que $h=1$ haciendo previamente una homotecia.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre