Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 1151
En el triángulo $ABC$ de área 100, $M$ es el punto medio del lado $AC$ y $P$
es un punto del lado $AB$ tal que el triángulo $AMP$ tiene área $36$. La paralela a $PM$ por $B$ corta al lado $AC$ en $Q$. Determinar el área del triángulo $MPQ$.
pistasolución 1info
Pista. Descompón $ABC$ en $AMP$, $BPM$ y $MBC$ y observa que $BPM$ y $MPQ$ tienen el mismo área.
Solución. El triángulo $ABC$ se puede descomponer en los triángulos $AMP$, $BPM$ y $MBC$. Sabemos que el área de $AMP$ es $36$ y la de $MBC$ es $50$ (por ser $M$ el punto medio de $AC$); como el área total es 100, deducimos que $BPM$ tiene área $100-50-36=14$. Finalmente, hay que darse cuenta de que $BPM$ y $MPQ$ tienen el mismo área ya que $BQ$ es paralela a $MP$. Por tanto, la respuesta es $14$.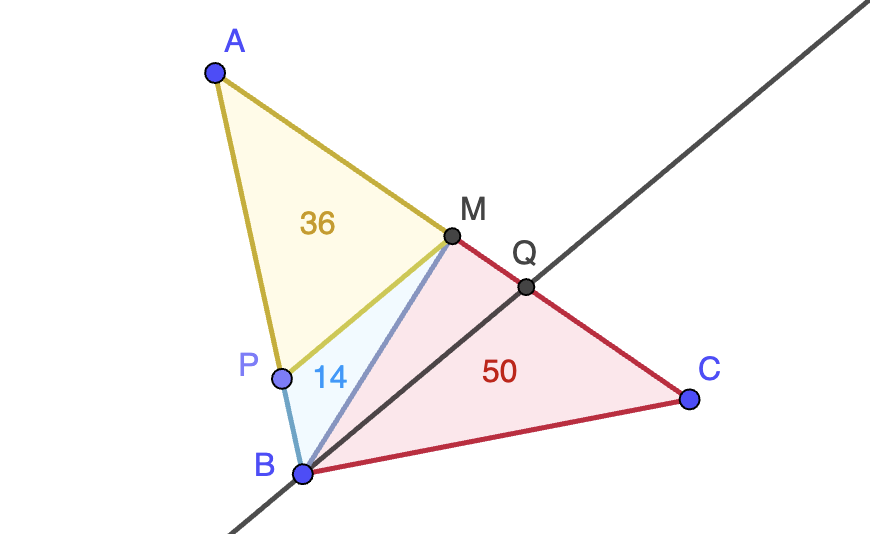

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre