Administración     

Olimpiadas de Matemáticas
Página de preparación y problemas

OME Local
OME Andaluza
OME Nacional
OIM
IMO
EGMO
USAMO
ASU
OMCC
Retos UJA
Selector
La base de datos contiene 2434 problemas y 940 soluciones.
Problema 1153
OME Local, 1998-P8
  1. Los vértices de un octógono regular se emparejan y se trazan los segmentos (lado o diagonal) que cada pareja determina. ¿Es posible emparejarlos de forma que los cuatro segmentos determinados tengan distintas longitudes?
  2. Demostrar que si se emparejan los vértices de un dodecágono regular y se trazan los segmentos que cada pareja determina, siempre habrá al menos dos con la misma longitud.
pistasolución 1info
Pista. Numera los vértices consecutivamente y mira la paridad de los números emparejados por cada tipo de segmento.
Solución. En el caso del octógono, tras algunos intentos es muy fácil llegar a una solución, por ejemplo la que se muestra en la imagen más abajo.

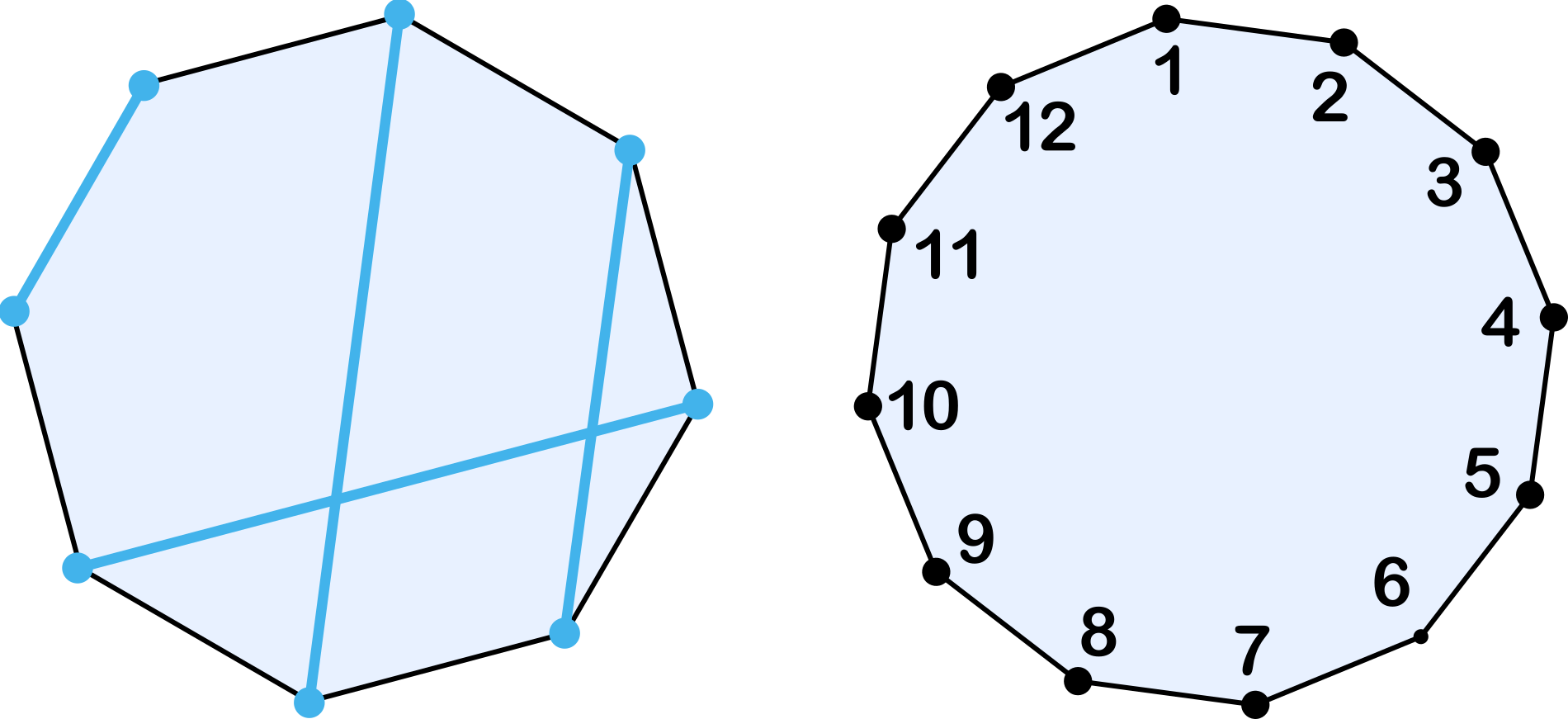
En el caso del dodecágono, para demostrar que no se puede, vamos a razonar por reducción al absurdo suponiendo que existen 6 segmentos de distinta longitud que emparejan los 12 vértices. Si numeramos los vértices consecutivamente con números del 1 al 12, habrá siempre 3 de los segmentos que unan un vértice par con uno impar mientras que los otros tres unirán par con par o bien impar con impar. Como entre 1 y 12 hay el mismo número de pares que de impares, hemos llegado a la contradicción buscada.

imagen

Nota. El mismo razonamiento prueba que es imposible el emparejamiento para polígonos de $8n+4$ vértices. ¿Es posible emparejar los vértices de un polígono de $8n$ lados? ¿Y los de un polígono de $4n+2$ lados?

Informar error
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2025. Esta página ha sido creada mediante software libre