Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Para el apartado (a), sea $ABCD$ un cuadrilátero convexo y $P$ el punto de corte de sus diagonales. Si llamamos $X$ e $Y$ las proyecciones de $A$ y $C$ sobre la diagonal $BD$, debe cumplirse que $AX=CY$ para que los triángulos $ABD$ y $BCD$ tienen la misma área (observemos que $BD$ actúa como base común de ambos triángulos). Como $AXP$ y $CYP$ son semejantes por estar en posición de Thales, se sigue que son congruentes y $AP=CP$. De la misma forma se prueba que $BP=DP$, luego las diagonales de $ABCD$ se cortan en su punto medio y el cuadrilátero tiene que ser un paralelogramo.

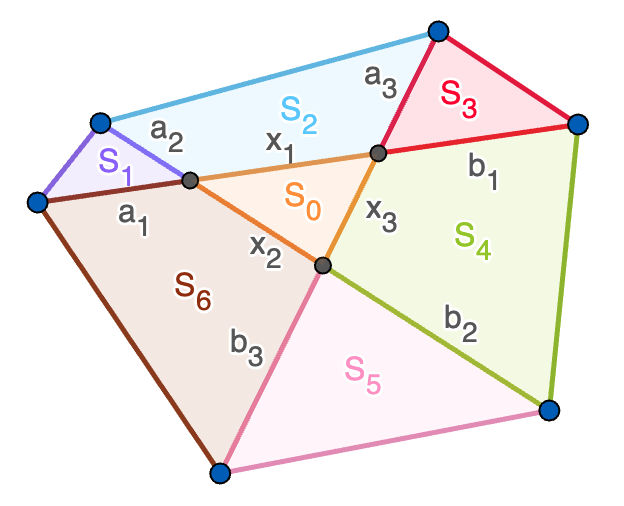
En cuanto al apartado (b), supongamos que tenemos un hexágono convexo que cumple la propiedad del enunciado pero no sabemos si las diagonales se cortan en el mismo punto. Estas diagonales dividen al hexágono en siete regiones de áreas $S_0,\ldots,S_6$ y denotamos por $a_1,a_2,a_3$, $b_1,b_2,b_3$ y $x_1,x_2,x_3$ los segmentos que se forman, todo ello como se indica en la figura. Las igualdades de las áreas se traducen en \begin{align*} S_1+S_2+S_3&=S_0+S_4+S_5+S_6,\\ S_3+S_4+S_5&=S_0+S_6+S_1+S_2,\\ S_5+S_6+S_1&=S_0+S_2+S_3+S_4. \end{align*} Sumando estas igualdades dos a dos, obtenemos que \[S_1=S_0+S_4,\qquad S_2=S_0+S_5,\qquad S_3=S_0+S_6,\] Tenemos que $S_1$ es el área de un triángulo que se puede calcular como la mitad del producto de $a_1$ y $a_2$ por el seno del ángulo que forman estos dos lados y que $S_0+S_4$ es el área de otro triángulo que análogamente es la mitad del producto de $x_1+b_1$ y $x_2+b_2$ por el seno del ángulo que forman estos dos segmentos. Los dos ángulos que se han considerado son opuestos por el vértice luego sus senos pueden simplificarse en la igualdad $S_1=S_0+S_4$, obteniendo que \[S_1=S_0+S_4\ \Longleftrightarrow\ a_1a_2=(b_1+x_1)(b_2+x_2)\] y de la misma forma \begin{align*} S_2=S_0+S_5&\ \Longleftrightarrow\ a_3b_1=(b_3+x_3)(a_1+x_1), S_3=S_0+S_6&\ \Longleftrightarrow\ b_2b_3=(a_2+x_2)(a_3+x_3). \end{align*} Multiplicando las tres igualdades así obtenidas, llegamos a que \[a_1a_2a_3b_1b_2b_3=(a_1+x_1)(a_2+x_2)(a_3+x_3)(b_1+x_1)(b_2+x_2)(b_3+x_3),\] pero como todos los números son positivos, el miembro de la derecha es estrictamente mayor que el de la izquierda a menos que $x_1=x_2=x_3=0$, lo que equivale a que las tres diagonales se corten en un único punto.