Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 1181
ASU, 1964-P10
Un círculo de centro $O$ está inscrito en un cuadrilátero $ABCD$. Demostrar que
\[\angle AOB+\angle COD=180^\circ.\]
pistasolución 1info
Pista. Si $M$ y $N$ son los puntos medios de $AB$ y $BC$, entonces fíjate en que $BOM$ y $NOB$ son congruentes.
Solución. Sean $M,N,P,Q$ los puntos medios de los lados $AB,BC,CD,DA$, respectivamente, tal y como se indica en la figura. Los triángulos $AMO$ y $BNO$ son congruentes ya que $MB=BN$ y $\angle MBO=\angle NBO$ por la tangencia y también $BO$ es común a ambos triángulos. Por esto, se tiene que $\angle MOB=\angle NOB$. De la misma manera, se prueba que $\angle NOC=\angle POC$, que $\angle POD=\angle DOQ$ y que $\angle QOA=\angle AOM$. En la figura, se indican con el mismo color ángulos iguales, luego está claro que $\angle AOB+\angle COD=180^\circ$ ya que esta suma tiene un ángulo de cada color y el doble sería el ángulo completo de $360^\circ$.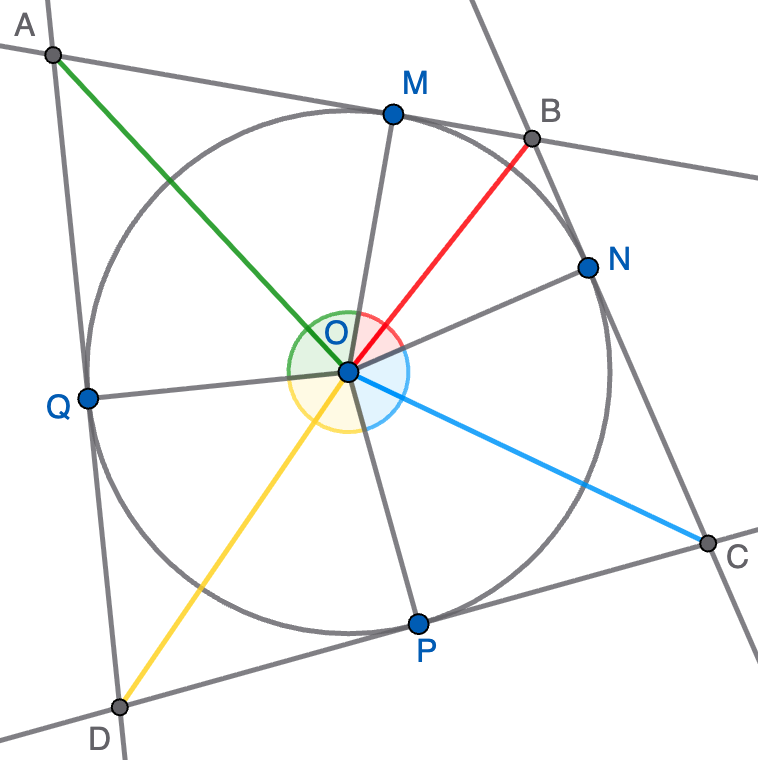

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre