Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 1417problema obsoleto
El impuesto sobre el Rendimiento del Trabajo Personal es una función $f(x)$ del total $x$ de las retribuciones anuales (en pesetas), de la que se conocen las siguientes propiedades:
- $f(x)$ es una función continua.
- La derivada $f'(x)$ en el intervalo $0\leq x\lt 60000$ es constante e igual a cero; en el intervalo $60000\lt x\lt P$ es constante e igual a $1$; y para $x\gt P$ es constante e igual a $0.14$.
- $f(0)=0$ y $f(140000) = 14000$.
pistasolución 1info
Pista. Observa que $f(x)$ es constante $0$ en $0\leq x\leq 60000$, es de la forma $x+a$ para $60000\leq x\leq P$ y de la forma $0.14x+b$ para $x\geq P$. Ajusta las constantes $a$ y $b$ usando la continuidad.
Solución. Como la derivada es cero para $0\leq x\lt 60000$ y $f(0)=0$, se deduce que $f(x)=0$ para $0\leq x\leq 60000$. En el intervalo $60000\lt x\lt P$, la derivada es constante $1$, luego la función es de la forma $f(x)=x+a$ para cierto número real $a$. Imponiendo por continuidad que $f(60000)=0$, llegamos a que $a=-60000$. Finalmente, como $f'(x)=0.14$ para $x\geq P$, tendrá que ser $f(x)=0.14x+b$ para todo $x\geq P$ y para cierta constante $b$. Para que esto concuerde por continuidad con el intervalo anterior, tenemos que
\[f(P)=P-60000=0.14P+b,\]
luego debe ser $b=0.84P-60000$. En resumidas cuentas, hemos probado que
\[f(x)=\begin{cases}0&\text{si }0\leq x\lt 60000,\\
x-60000&\text{si }60000\leq x\leq P,\\
0.14x+0.86P-60000&\text{si }x\geq P.\end{cases}\]
Ahora bien, como $f(140000)=14000\neq 140000-60000$, no puede ser $140000\leq P$, luego ha de ser $140000\gt P$ y se aplica la tercera línea de la definición de $f(x)$, es decir,
\[14000=f(140000)=0.14\cdot 140000+0.84 P-60000.\]
Esta ecuación de primer grado tiene solución $P=\frac{2720000}{43}\approx 63255.8$.
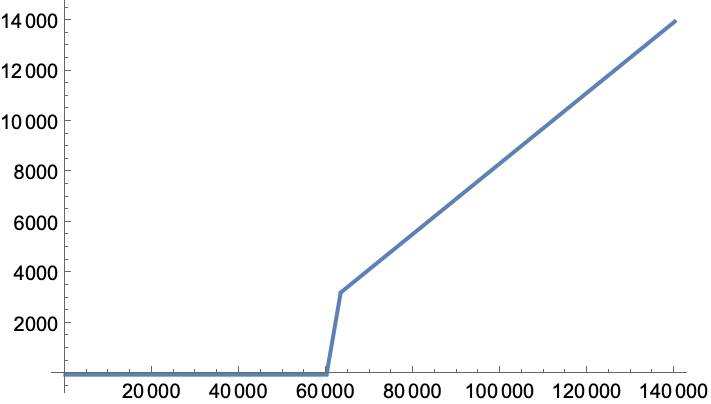
Para representar la gráfica de la función, solo hay que darse cuenta de que está formada por tres trozos rectilíneos: el primero es la constante cero, el segundo tiene pendiente $1$ que pasa por el punto $(60000,0)$ y el tercero tiene pendiente $0.14$ y pasa por $(140000,14000)$. Queda así una gráfica como se muestra en la figura.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre