Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 1564
Sean $C$ y $C'$ dos circunferencias concéntricas de radios $r$ y $r'$, respectivamente. Determinar cuánto ha de valer el cociente $r'/r$ para que en la corona limitada por $C$ y $C'$ existan ocho circunferencias $C_1,C_2,\ldots,C_8$ que sean tangentes a $C$ y $C'$ y también que cada $C_i$ sea tangente exterior a $C_{i+1}$ para $1\leq i\leq 7$ y $C_8$ sea tangente exterior a $C_1$.
pistasolución 1info
Pista. Resuelve el triángulo cuyos vértices son el centro común de $C$ y $C'$, el centro de $C_1$ y el punto de tangencia de $C_1$ y $C_2$.
Solución. Supondremos que $C'$ es la circunferencia exterior. Por simetría, cada una de las circunferencias $C_1,C_2,\ldots,C_8$ tiene que estar inscrita en un sector angular de $45^\circ$. Todas ellas tienen que tener el mismo radio, que llamaremos $\rho$ y debe cumplirse que $r'=r+2\rho$ ya que un radio de $C'$ se puede expresar como suma de un radio de $C$ y del diámetro de cualquier $C_i$. Además, considerando el triángulo indicado en la figura, podemos calcular el seno de $22,5^\circ$ como el cateto opuesto $\rho$ dividido por la hipotenusa $r+\rho$. El seno de este ángulo se puede calcular por la fórmula del ángulo mitad (ver la nota), lo que nos da
\[\tfrac{1}{2}\sqrt{2-\sqrt{2}}=\operatorname{sen}(22.5)=\frac{\rho}{r+\rho}=\frac{r'-r}{r'+r}=\frac{\frac{r'}{r}-1}{\frac{r'}{r}+1},\]
luego podemos despejar
\[\frac{r'}{r}=\frac{1+\tfrac{1}{2}\sqrt{2-\sqrt{2}}}{1-\tfrac{1}{2}\sqrt{2-\sqrt{2}}}=7-4 \sqrt{2}+2 \sqrt{20-14 \sqrt{2}}.\]
¿Sabrías justificar esta última racionalización?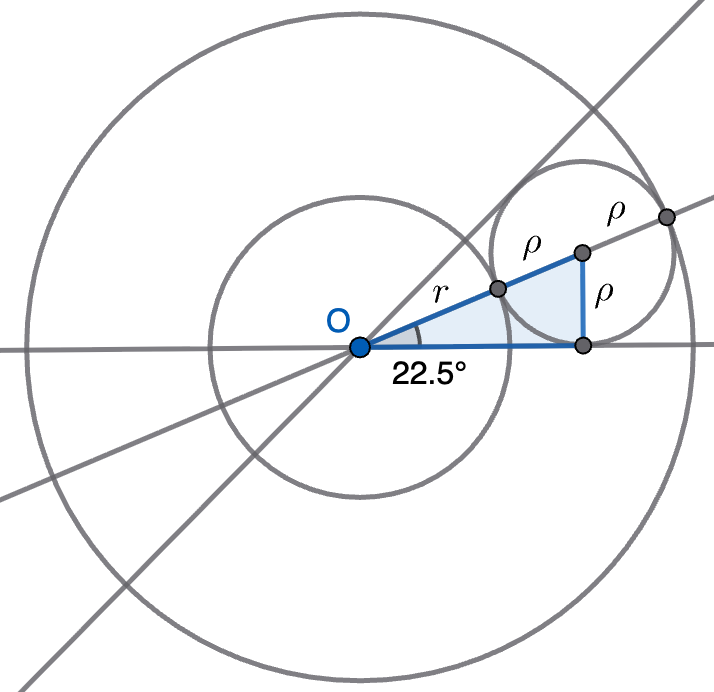

Nota. La fórmula del seno del ángulo mitad nos dice que \[\operatorname{sen}^2(\tfrac{x}{2})=\frac{1-\cos(x)}{2}.\] En el caso $x=45$, hay que darse cuenta también de que $\operatorname{sen}(\tfrac{x}{2})$ es positivo.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre