Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 1580
En el plano tenemos una recta $r$ y dos puntos $A$ y $B$ que no pertenecen a $r$ pero se encuentran en el mismo semiplano determinado por ella. Determinar un punto $M$ de la recta tal que el ángulo de $r$ con $AM$ sea doble del de $r$ con $BM$ (considerando como ángulo de dos rectas el menor de los ángulos que forman).
pistasolución 1info
Pista. Intenta que $BM$ sea la bisectriz del ángulo que forman $r$ y $AM$ y procura no dejar ningún caso sin analizar.
Solución. Trazamos la circunferencia $\Gamma$ de centro $B$ que es tangente a $r$, la semicircunferencia de $\Gamma$ más distante de $r$ (marcada en azul en la figura superior) y la región entre dicha circunferencia y $r$ (marcada en rosa en la figura superior). También consideramos las semirrectas paralelas a $r$ que se proyectan fuera de $\Gamma$ (marcadas en verde en la figura superior). Distinguimos dos casos:
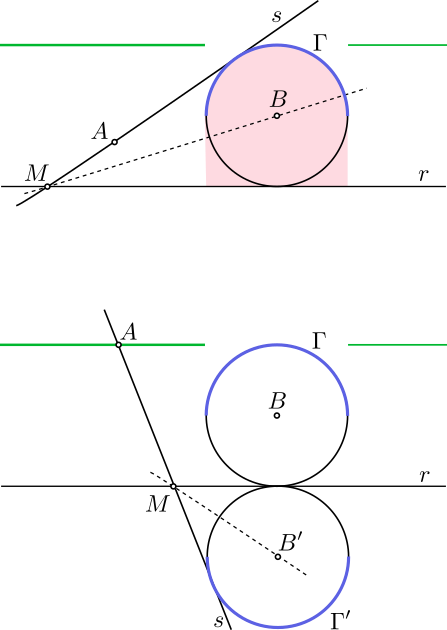
- Supongamos que $A$ no está en la región marcada en rosa. Entonces trazamos una recta tangente $s$ a $\Gamma$ que pase por $A$ y corte a $\Gamma$ en la semicircunferencia azul.
- Si $A$ no está en ninguna de las dos semirrectas paralelas a $r$ marcadas en verde, entonces podemos tomar $s$ que no sea paralela a $r$ y definimos $M$ como el punto de corte de $s$ y $r$. Entonces, $BM$ es la bisectriz del ángulo (menor de $90^\circ$) que forman $r$ y $AM$, luego se cumple la propiedad que queremos.
- Si $A$ está en una de las semirrectas marcadas en verde, entonces tomamos la circunferencia $\Gamma'$ simétrica de $\Gamma$ respecto de $r$ y $s$ una tangente a $\Gamma'$ en un punto de la semicircunferencia simétrica del original. Definimos de nuevo $M$ como el punto de corte de $s$ y $r$. Como $MB'$ es la bisectriz del ángulo menor de $90^\circ$ que forman $r$ y $s'$, se tiene que el ángulo que forman $MB$ y $r$ es igual al que forman $MB'$ y $r'$ y por tanto también se cumple la propiedad.
- Supongamos ahora que $A$ está en la región marcada de rojo. Entonces, las tangentes a $\Gamma$ o $\Gamma'$ son las únicas candidatas a cumplir la propiedad que deseamos y todas ellas la cumplen pero solo si consideramos el ángulo mayor que forman con $r$, no el menor como se especifica en el enunciado. Concluimos que en este caso el problema no tiene solución.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre