Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 1679
Dadas dos circunferencias exteriores de radios $r$ y $r'$ ($r\neq r'$), se pide dibujar, razonadamente, una recta paralela a una dirección dada, tal que determine sobre las dos circunferencias dos cuerdas tales que la suma de sus longitudes sea igual a una longitud dada $\ell$.
pistasolución 1info
Pista. Quédate con dos semicírculos de forma que el problema se reduzca a que la suma de longitudes sea $\frac{\ell}{2}$.
Solución. Por simplicidad, supongamos que la dirección dada es la horizontal y que el centro $O$ de la circunferencia $\Gamma$ de radio $r$ está a la izquierda (o sobre la misma vertical) que el centro de la circunferencia $\Gamma'$ de radio $r'$. Cortamos $\Gamma$ y $\Gamma'$ por sus diámetros verticales y consideramos $C$ la semicircunferencia izquierda de $\Gamma$ y $C'$ la semicircunferencia derecha de $\Gamma'$. Trasladamos horizontalmente $C'$ hasta otra semicircunferencia $C''$ para que su diámetro se superponga con el de $C$, creando así la figura sombreada en la imagen. Como esta figura está compuesta por dos semicírculos, será suficiente encontrar un segmento en la dirección dada de longitud $\frac{\ell}{2}$. Para ello sólo hay que desplazar la figura una distancia $\frac{\ell}{2}$ a la derecha y tomar los puntos $X$ donde el borde de figura trasladada (en rojo en la imagen) se corte con el borde original (en verde). Por estos puntos $X$ pasarán las rectas que buscamos.
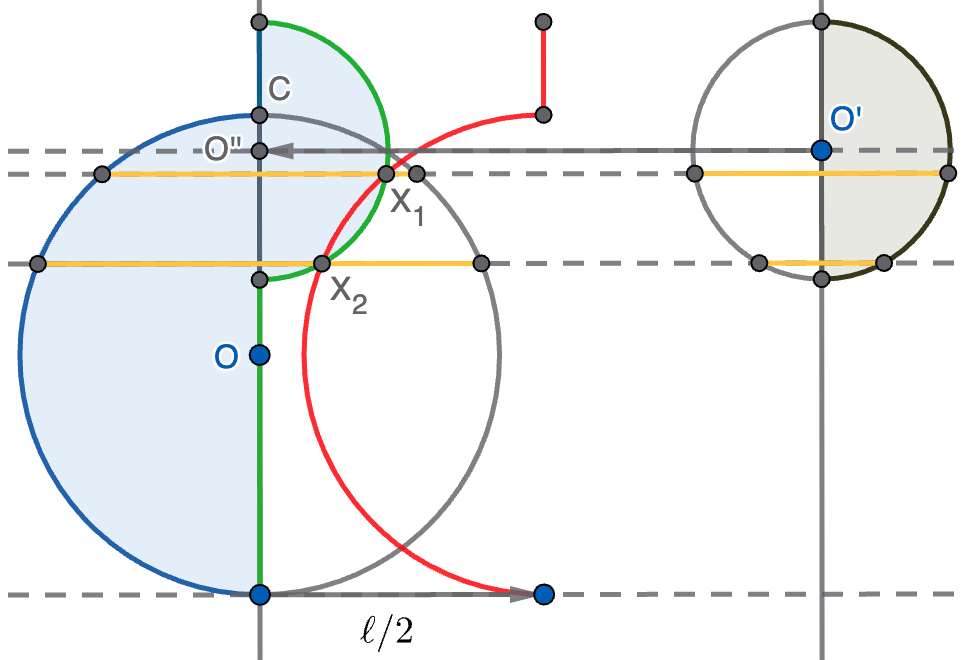
En la imagen se tiene un ejemplo, donde hay exactamente dos soluciones $X_1$ y $X_2$, para cada una de las cuales se ha indicado los segmentos cuyas longitudes suman $\ell$ en amarillo.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre