Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 2096
OMCC, 2010-P4
Encontrar todos los enteros positivos $N$ tales que un tablero $N\times N$ se puede recubrir usando piezas de tamaño $5\times 5$ o $1\times 3$.
pistasolución 1info
Pista. Observa que si puedes recubrir un tablero $N\times N$, también puedes recubrir fácilmente un tablero $(N+3)\times(N+3)$.
Solución. Comenzamos observando que los tableros $3\times 3$ y $5\times 5$ se pueden recubrir fácilmente y tampoco es difícil dar con un recubrimiento del tablero $7\times 7$, como se muestra en la figura. Además, dado un tablero $N\times N$ que se pueda recubrir, también se puede recubrir uno de dimensiones $(N+3)\times(N+3)$ pues basta con rodearlo rellenar las columnas nuevas con fichas $1\times 3$ todas orientadas en horizontal y las casillas restantes de las tres filas nuevas con fichas $3\times 1$ todas en vertical (como se muestra en la figura de abajo). Esto nos deja solo por comprobar los tableros de tamaño $1\times 1$, $2\times 2$ y $4\times 4$, que claramente no se pueden recubrir ya que el número de casillas es menor de $25$ y no es múltiplo de $3$.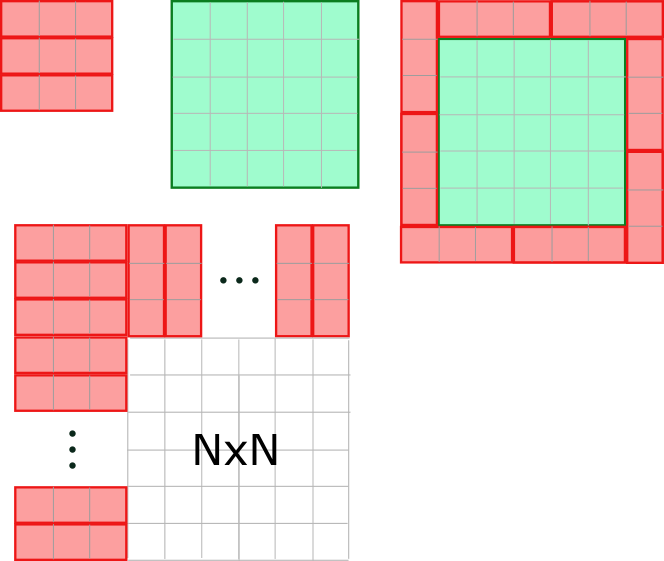

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre