Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
Como $ADPF$ es cíclico, tenemos que $\angle APD=\angle AFD=180-\alpha-\delta$ y, como $ABPE$ es cíclico, tenemos que $\angle APB=\angle AEB=180-\alpha-\beta$, luego
\[\angle DPB=\angle DPA+\angle APB=(180-\alpha-\delta)+(180-\alpha-\beta)=360-2\alpha-\beta-\delta=\gamma-\alpha,\]
donde hemos usado que $\alpha+\beta+\gamma+\delta=360$. Ahora bien, como $ADPF$ es cíclico, tenemos que $\angle DPF=180-\angle DAF=180-\alpha$, luego obtenemos que
\[\angle BPF=\angle DPF-\angle APF=(180-\alpha)-(\gamma-\alpha)=180-\gamma=\angle BCF.\]
De este modo, los dos ángulos indicados en rojo en la figura son iguales, luego $P$ está en la circunferencia circunscrita al triángulo $BFC$. Con la circunferencia $DCE$ se razona igual (sólo hay que cambiar $E$ por $F$ y $B$ y $\beta$ por $D$ y $\delta$ en el razonamiento anterior).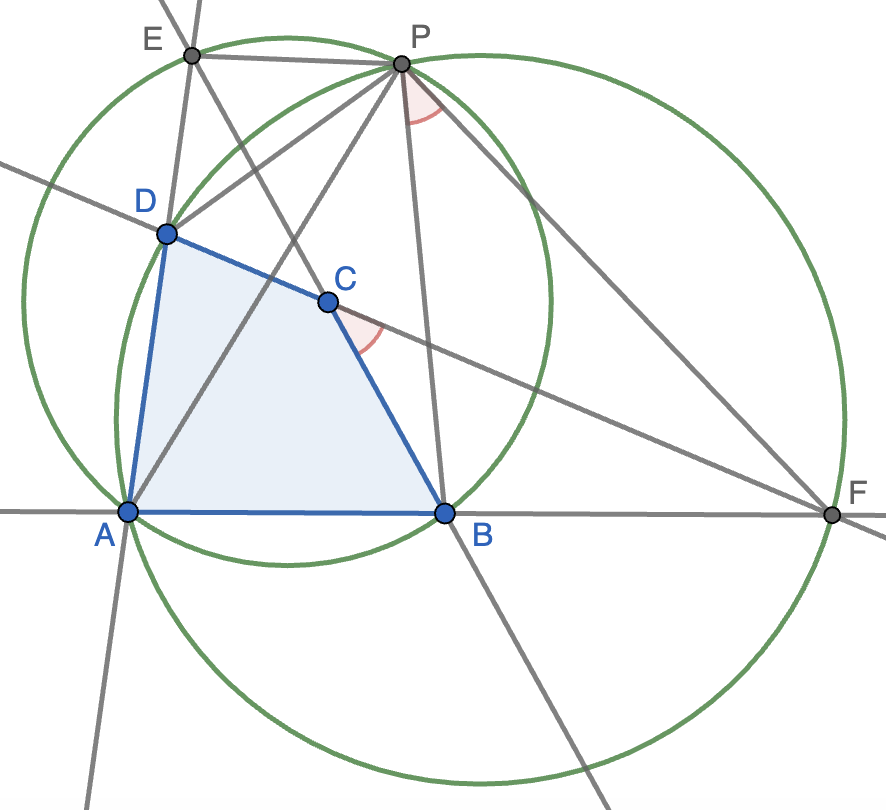
Informar de error en enunciado Informar de procedencia del problema