Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 2315
Sea $ABC$ un triángulo acutángulo cuyos lados tienen longitudes $a$, $b$ y $c$ y sea $S$ el área del triángulo. Sea $P$ un punto interior del triángulo de forma que
\[a\cdot PA+b\cdot PB+c\cdot PC=4S.\]
Demostrar que $P$ es el ortocentro del triángulo $ABC$.
pistasolución 1info
Pista. Demuestra que $a\cdot PA+b\cdot PB+c\cdot PC\geq 4S$ para cualquier punto P$ interior, para lo que puede ser útil ver los productos $a\cdot PA$, $b\cdot PB$ y $c\cdot PC$ como áreas. Luego estudia qué tiene que ocurrir para que se alcance la igualdad.
Solución. Trazamos por cada vértice del triángulo una paralela al lado opuesto y definimos los puntos $A',B',C'$ como los pies de las perpendiculares desde $P$ a estas tres rectas, como se muestra en la figura. Tenemos entonces que
\begin{align*}
\mathrm{Area}(ACPB)&=\mathrm{Area}(ABC)-\mathrm{Area}(BPC)=\tfrac{1}{2}a\cdot PA',\\
\mathrm{Area}(CBPA)&=\mathrm{Area}(ABC)-\mathrm{Area}(ABP)=\tfrac{1}{2}b\cdot PB',\\
\mathrm{Area}(BAPC)&=\mathrm{Area}(ABC)-\mathrm{Area}(CPA)=\tfrac{1}{2}c\cdot PC',
\end{align*}
ya que $PA',PB',PC'$ representan la diferencia de alturas de los triángulos cuyas áreas se restan y $a,b,c$ sus bases. Si sumamos las áreas de estos tres cuadriláteros cóncavos, obtenemos dos veces el área de $ABC$, luego esta suma nos da
\[4S=a\cdot PA'+b\cdot PB'+c\cdot PC'.\]
Sin embargo, tenemos que $PA'\leq PA$ ya que $APA'$ es un triángulo rectángulo en el que $PA'$ es un cateto y $PA$ es la hipotenusa. De la misma manera, se cumple que $PB'\leq PB$ y $PC'\leq PC$. En consecuencia,
\[4S\leq a\cdot PA+b\cdot PB+c\cdot PC\]
para cualquier punto $P$ interior al triángulo. Para que la igualdad se alcance, en los triángulos rectángulos $APA'$, $BPB'$ y $CPC'$ tiene que ser $AA'=BB'=CC'=0$, luego $PA=PA'$ es perpendicular a $BC$, $PB=PB'$ es perpendicular a $AC$ y $PC=PC'$ es perpendicular a $AB$. En definitiva, la igualdad se cumple si y sólo si $P$ es está en las tres alturas del triángulo, es decir, sólo si $P$ es el ortocentro.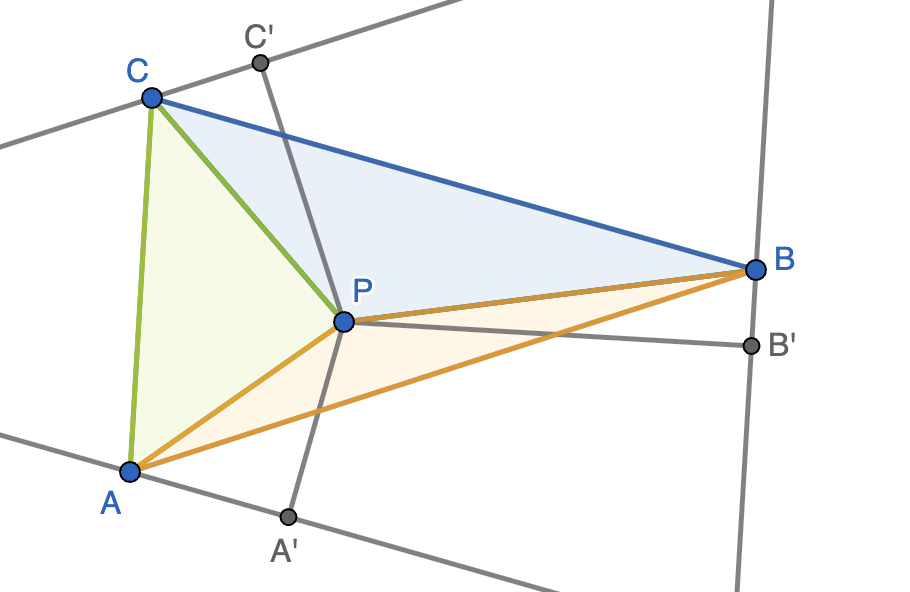

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre