Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 2320
En un triángulo $ABC$, se eligen un punto $X$ en el lado $AB$ y otro punto $Y$ en el lado $AC$ alineados con el baricentro $G$ del triángulo. Hallar el menor número real $k$ que verifica la desigualdad
\[BX\cdot CY\leq k\cdot AX\cdot AY,\]
para cualesquiera $X$ e $Y$ en las condiciones dadas.
pistasolución 1info
Pista. Transforma la desigualdad en una desigualdad entre las áreas de los triángulos $CGQ$, $AGQ$, $BGP$ y $AGP$.
Solución. Llamemos $S_1$, $S_2$, $S_3$, $S_4$ a las áreas de los triángulos $CGQ$, $AGY$, $BGX$ y $AGX$, respectivamente, que se encuentran coloreadas en la figura. Como $CGY$ y $AGY$ tienen una altura común y también la tienen $BGX$ y $AGX$ (estas alturas comunes están dibujadas en línea discontinua azul), tenemos que
\[\frac{XB}{XA}\cdot\frac{YC}{YA}=\frac{S_4}{S_3}\cdot\frac{S_1}{S_2}.\]
Ahora vamos a calcular estas áreas de otra forma, para lo que trazamos las alturas $AA'$, $BB'$ y $CC'$, siendo $A',B',C'$ puntos de la recta que pasa por $G$. Tenemos entonces que
\[\frac{S_4}{S_3}\cdot\frac{S_1}{S_2}=\frac{BB'\cdot CC'}{(AA')^2}.\]
Ahora bien, como $M$ es el punto medio de $BC$, la altura $MM'$ del triángulo $MXY$ (en gris discontinuo) cumple que $MM'=\frac{1}{2}(BB'+CC')$. El área de $MXY$ es $\frac{1}{2}MM'\cdot XY$ y el área de $AXY$ es $\frac{1}{2}XY\cdot AA'$. Como el área de $AXY$ es el doble que la de $MXY$ (ya que el baricentro divide a la mediana en dos segmentos tales que $AG=2GM$), tenemos que $\frac{1}{2}(BB'+CC')=MM'=\frac{1}{2}AA'$, de donde $AA'=BB'+CC'$. Finalmente, esto nos dice que
\[\frac{XB}{XA}\cdot\frac{YC}{YA}=\frac{BB'\cdot CC'}{(AA')^2}=\frac{BB'\cdot CC'}{(BB'+CC')^2}=\frac{1}{2+\frac{BB'}{CC'}+\frac{CC'}{BB'}}\leq\frac{1}{4},\]
donde hemos usado que la suma de un número positivo y su inverso es mayor o igual que $2$. La igualdad se alcanza cuando $BB'=CC'$, es decir, cuando la recta $XY$ es paralela al lado $BC$, luego la constante $k=\frac{1}{4}$ es la elección óptima para cualquier triángulo.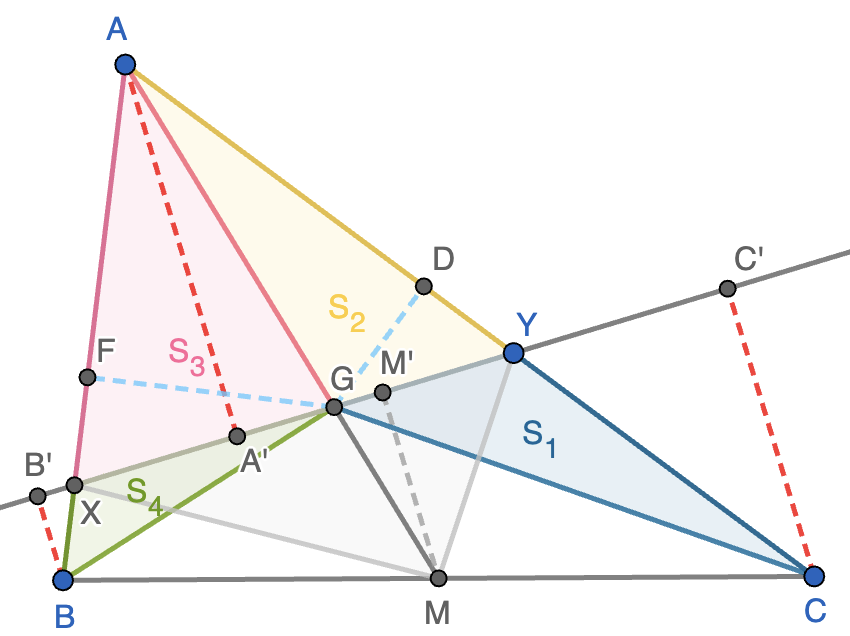

Nota. Este problema es una reformulación del problema 3 de la fase nacional de la Olimpiada Matemática Española de 1995.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre