Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 2732
Dos jugadores juegan en un tablero infinito de casillas $1\times 1$. El jugador A elige una casilla y pone en ella una O. A continuación el jugador B elige otra casilla y pone en ella una X. Juegan así por turnos hasta que uno de los jugadores llena una fila o una columna de cinco casillas consecutivas, en cuyo caso gana el juego. Demostrar que el jugador B puede impedir que el jugador A gane el juego.
pistasolución 1info
Pista. Piensa en teselar el tablero completo con piezas $2\times 1$ y $1\times 2$.
Solución. Consideramos una teselación del plano infinito por piezas de tamaño $2\times 1$ y $1\times 2$ formando escaleras infinitas, como se muestra en la figura. Cada vez que A coloca en una casilla, la estrategia de B es colocar en la otra casilla de la misma pieza. De esta forma, A nunca puede conseguir 5 en fila porque cualquier rectángulo $5\times 1$ o $1\times 5$ contiene completamente a alguna de las piezas $2\times 1$ o $1\times 2$, respectivamente.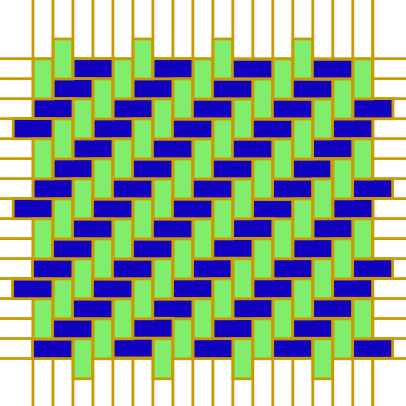

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre