Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1075 soluciones.
Problema 2733
Sean $a,b,c\in(0,\frac{\pi}{2})$ las raíces de las ecuaciones
\[\cos(x)=x,\qquad \mathrm{sen}(\cos(x))=x,\qquad \cos(\mathrm{sen}(x))=x,\]
respectivamente. Ordenar de menor a mayor los tres números $a,b,c$, justificando la respuesta.
pistasolución 1info
Pista. Utiliza que $\operatorname{sen}(x)\lt x$ para todo $x\in(0,\frac{\pi}{2})$.
Solución. Como $\operatorname{sen}(x)\lt x$ para todo $x\in(0,\frac{\pi}{2})$ y el coseno es una función decreciente, tenemos la cadena de desigualdades
\[\operatorname{sen}(\cos(x))\lt\cos(x)\lt\cos(\operatorname{sen}(x)).\]
Por tanto, los puntos en que estas funciones cortan a la recta $y=x$ estarán en el mismo orden que las funciones, es decir, $b\lt a\lt c$ (en la imagen puede verse una representación gráfica de las tres funciones y la recta).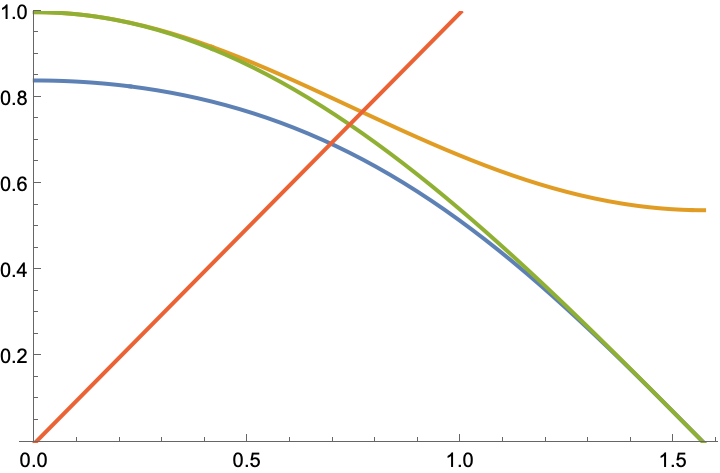

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre