Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 2735
Se da un cono de revolución cuyo ángulo en el vértice es de $60^\circ$. En este cono se van introduciendo esferas, de forma que la primera quede tangente al cono, la segunda tangente al cono y a la primera esfera, la tercera tangente al cono y a la segunda esfera, y así sucesivamente. El radio de la primera esfera se denota por $r_1$. Se pide calcular:
- El radio $r_n$ de la esfera introducida en $n$-ésimo lugar.
- El volumen comprendido entre el cono y las esferas introducidas en los lugares $n$-ésimo y $(n+1)$-ésimo.
pistasolución 1info
Pista. Puedes trabajar en una figura bidimensional ya que todo el problema es invariante por rotaciones respecto del eje del cono. Busca la homotecia que te lleva una esfera en la otra y expresa el volumen usando conos truncados y casquetes esféricos.
Solución. Dado que toda la figura es de revolución, podemos simplificar el razonamiento pensando en un objeto bidimensional que debe ser rotado respecto de un eje. Denotamos por $O_n$ el centro de la circunferencia $n$-ésima, por $T_n$ el punto de tangencia con una de las directrices del cono y por $P_{n+1}$ el punto de tangencia con la circunferencia $(n+1)$-ésima, como se indica en la figura. Dado que los radios que pasan por los puntos de tangencia son perpendiculares a la recta de tangencia, se tiene que $O_nT_nT_{n+1}O_{n+1}$ es un trapecio con ángulos rectos en $T_n$ y $T_{n+1}$, ángulo de $60^\circ$ en $O_{n+1}$. Por lo tanto, se verifica que
\[\frac{1}{2}=\cos(60)=\frac{r_{n+1}-r_n}{r_{n+1}+r_n}\ \Longleftrightarrow\ r_{n+1}=3r_n.\]
En otras palabras, cada radio es el triple del anterior, luego se tiene que $r_n=3^{n-1}r_1$ y hemos respondido al primer apartado.
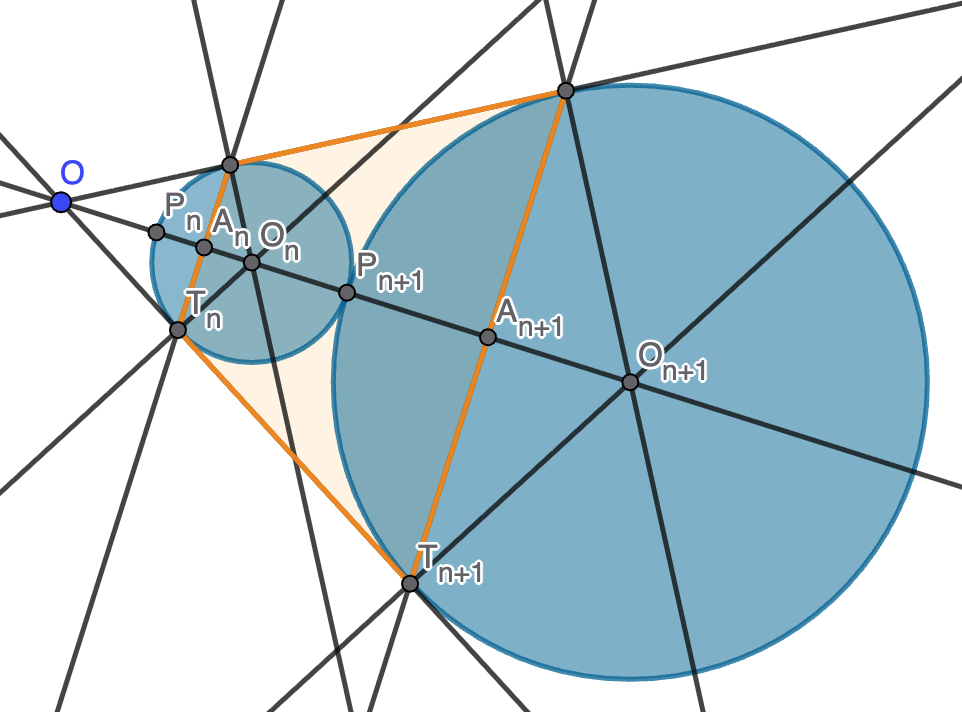
En cuanto al volumen, observamos que éste se puede calcular como el del cono truncado que surge al revolucionar la región naranja al que hay que quitarle dos casquetes esféricos, uno de la esfera $n$-ésima y otro de la esfera $(n+1)$-ésima. Vamos por partes:
- En el triángulo $OT_nO_n$ podemos calcular $\tan(30)=\frac{r_n}{OT_n}$, de donde $OT_n=r_n\sqrt{3}$. Ahora en el triángulo $OA_nT_n$ podemos calcular $A_nT_n=OT_n\operatorname{sen}(30)=\frac{\sqrt{3}}{2}r_n$ y $OA_n=OT_n\cos(30)=\frac{3}{2}r_n$. Por tanto, el cono de revolución del triángulo $OA_nT_n$ tiene volumen $V_n=\frac{1}{3}\pi(A_nT_n)^2(OA_n)=\frac{3}{8}\pi r_n^3$. El volumen de revolución del trapecio naranja será $V_{n+1}-V_n=\frac{3}{8}\pi(r_{n+1}^3-r_n^3)=\frac{39}{4}\pi r_n^3$.
- Como el triángulo $O_{n+1}P_{n+1}T_{n+1}$ es equilátero, $A_{n+1}$ es el punto medio de $P_{n+1}O_{n+1}$. Esto nos dice que buscamos el volumen de un casquete de la esfera $(n+1)$-ésima de altura la mitad su radio. La fórmula para el volumen del casquete nos da $\frac{5}{24}\pi r_{n+1}^3=\frac{45}{8}\pi r_n^3$.
- El mismo casquete en la esfera $n$-ésima tiene volumen $\frac{5\pi}{24}r_n^3$, pero en este caso necesitamos el casquete complementario, cuyo volumen será $\frac{4}{3}\pi r_n^3-\frac{5}{24}\pi r_n^3=\frac{9}{8}\pi r_n^3$.
Con todo esto, el volumen que buscamos para el apartado (b) es \[\frac{39}{4}\pi r_n^3-\frac{45}{8}\pi r_n^3-\frac{9}{8}\pi r_n^3=3\pi r_n^3.\]

Nota. El volumen de un casquete esférico de altura $h$ en una esfera de radio $r$ es $\frac{\pi}{3}h^2(3r-h)$.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre