Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1075 soluciones.
Problema 424
OIM, 1989-P2
Sean $x,y,z$ tres números reales tales que $0\lt x\lt y\lt z\lt\frac{\pi}{2}$. Demostrar la siguiente desigualdad:
\[\frac{\pi}{2}+2\sin(x)\cos(y)+2\sin(y)\cos(z)\gt \sin(2x)+\sin(2y)+\sin(2z).\]
pistasolución 1info
Pista. Interpreta cada uno de los términos como el área de una figura plana.
Solución. Consideremos un cuarto de circunferencia donde hemos representado los valores de $x,y,z$ como ángulos tal y como muestra la figura. Entonces, el área del rectángulo rojo está dada por $\cos(z)\mathrm{sen}(z)=\frac{1}{2}\mathrm{sen}(2z)$, el área del rectángulo verde por $(\cos(y)-\cos(z))\mathrm{sen}(y)=\frac{1}{2}\mathrm{sen}(2y)-\mathrm{sen}(z)\cos(y)$ y la del rectángulo azul por $(\cos(x)-\cos(y))\mathrm{sen}(x)=\frac{1}{2}\mathrm{sen}(2x)-\mathrm{sen}(x)\cos(y)$. Entre todas suman menos que el área del cuarto de círculo $\frac{\pi}{4}$, de donde claramente se deduce la desigualdad del enunciado.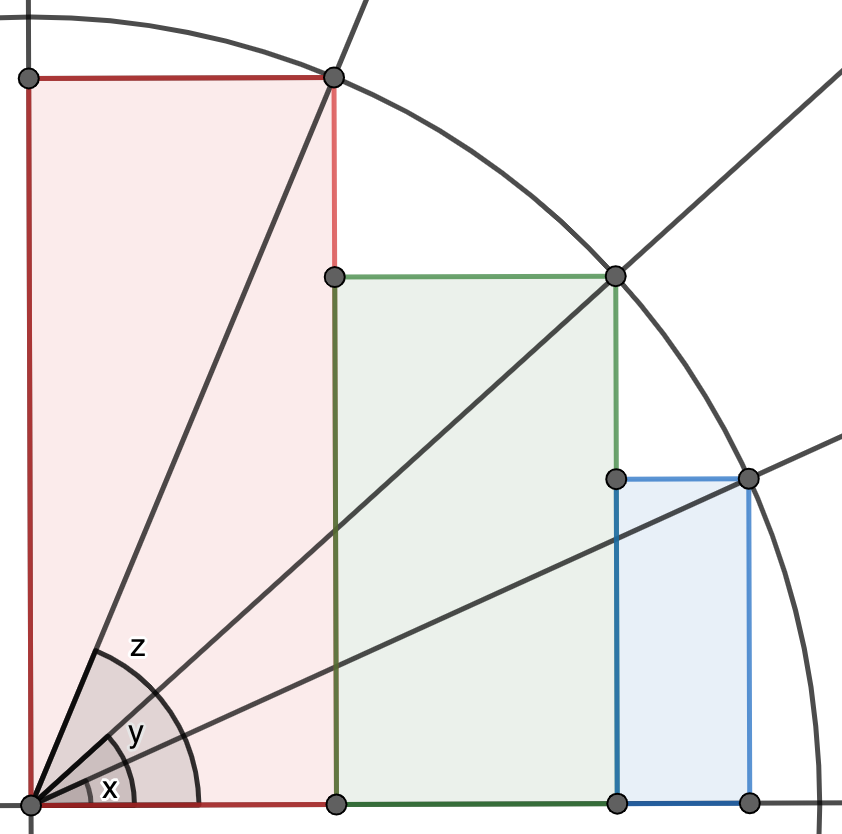

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre