Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2764 problemas y 1057 soluciones.
Problema 445
ASU, 1961-P1
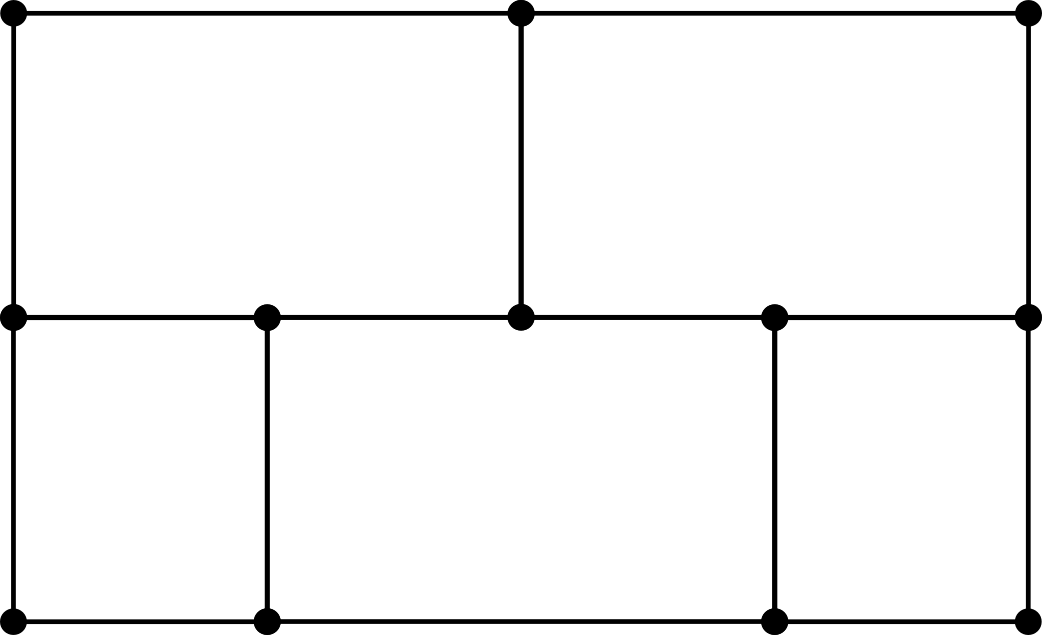
Consideramos la siguiente figura formada por 12 vértices y 16 segmentos. ¿Es posible dibujar una curva que atraviese cada segmento una única vez sin pasar por ningún vértice?
pistasolución 1solución 2info
Pista. ¿Qué pasa con la curva en las regiones con un número impar de lados?
Solución. Observemos que en la figura se forman tres pentagonos y dos cuadrados. Evidentemente, nuestra curva tendría que empezar fuera de (al menos) dos de los pentágonos. Cada vez que la curva atraviesa un lado de uno de estos pentágonos pasará de estar en el interior a estar en el exterior o del exterior al interior. Por tanto, como cada pentágono tiene un número impar de lados, la curva debería terminar en el interior de dos de los pentágonos, lo cual es absurdo. Concluimos que no existe dicha curva.
Solución. Esta es una solución muy estándar usando algo de teoría de grafos. La figura del enunciado es un grafo plano y podemos considerar el grafo dual, que tiene un vértice por cada cara del grafo original y en el que dos vértices se unen por una arista cuando representan a caras adyacentes (ver figura).
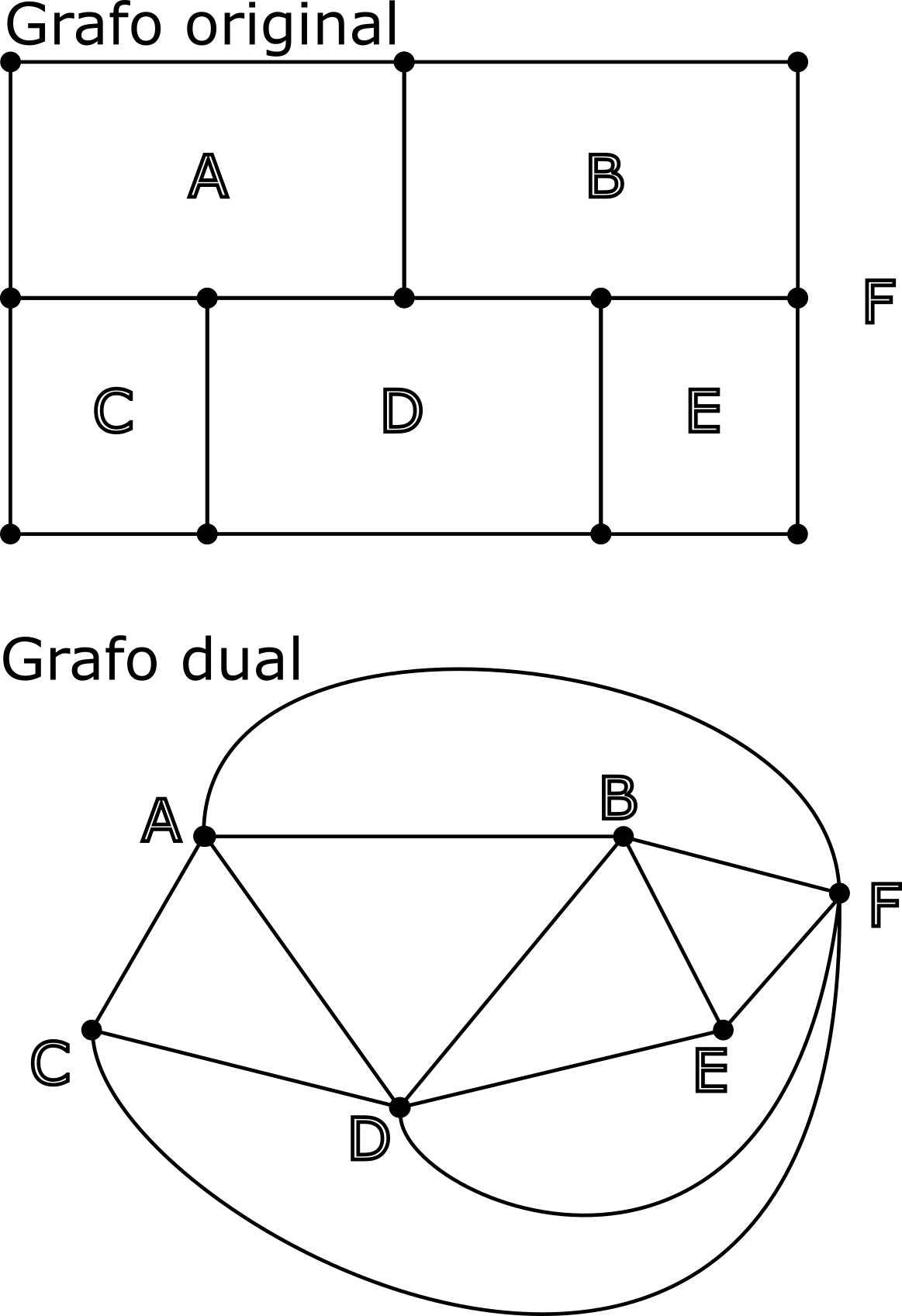
Atravesar una arista del grafo original equivale a recorrer una arista del grafo dual, por lo que el problema se reduce a encontrar un camino que pase por todas las aristas del grafo dual una sola vez. Esto no puede hacerse ya que eso implicaría que hay como máximo dos vértices del grafo dual a los que llegan un número par de aristas (Teorema de Euler). Sin embargo, el grafo dual tiene 4 vértices (C, D, E y F) a los que llegan un número par de aristas, por lo que concluimos que la curva buscada no puede existir.

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre