Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 459
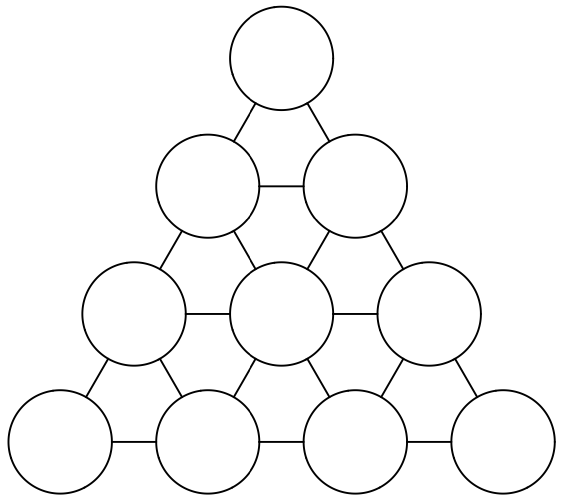
Sobre un tablero en forma de triángulo equilátero con un número par de filas $n$ (tal como se indica en la figura para $n=4$), se juega un solitario. Sobre cada casilla se coloca una ficha. Cada ficha es blanca por un lado y negra por el otro. Inicialmente, sólo una ficha, que está situada en un vértice, tiene la cara negra hacia arriba; las demás fichas tienen la cara blanca hacia arriba. En cada movimiento del juego se retira solamente una ficha negra del tablero y se da la vuelta a cada una de las fichas que ocupa una casilla vecina. Después de varios movimientos, ¿será posible quitar todas las fichas del tablero?
pistasolución 1info
Pista. Cada ficha es vecina de un número par de fichas.
Solución. Cada casilla es vecina de un número par de fichas (las del interior tienen 6 vecinas, las de los lados tienen 4 y las de los vértices tienen 2). Por tanto, si una ficha concreta resulta ser la última en retirarse, antes hemos tenido que quitar todas sus vecinas, lo que supone un número par de cambios de color. Esto nos dice que al proceder a retirar la última, su color es blanco y no puede retirarse. La respuesta a la pregunta del enunciado es, por tanto, negativa.
Nota. ¿Se pueden retirar todas las fichas menos una?
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre