Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Sean $P$, $Q$ y $R$ los pies de las alturas de $ABC$ sobre los lados $AB$, $AC$ y $BC$, respectivamente y llamemos $\alpha$, $\beta$ y $\gamma$ a los ángulos de $ABC$ por simplicidad. Vamos a suponer en primer lugar que el triángulo es acutángulo (primera figura). Como el cuadrilátero $APHQ$ tiene dos ángulos rectos, deducimos que $\angle PHQ=\pi-\beta$, luego $\angle CHQ=\beta$. Esto nos dice que los triángulos $CHQ$ y $ABQ$ son semejantes, luego tenemos que $\frac{CH}{HQ}=\frac{AB}{BQ}$. Por hipótesis, estamos suponiendo que $AB=CH$, luego $HQ=BQ$. Es inmediato entonces que $BHQ$ es un triángulo rectángulo isósceles, de donde $\angle HBQ=\frac{\pi}{4}$. Contando ángulos en el triángulo $BRC$, llegamos a que $\gamma=\frac{\pi}{4}$, lo que responde a la pregunta del enunciado.

Supongamos ahora que $\alpha=\frac\pi2$ (se razona igualmente para $\beta=\frac\pi2$), en cuyo caso se tiene que $A=H$ y $ABC$ es un triángulo rectángulo isósceles, de donde también tenemos que $\gamma=\frac{\pi}{4}$. Otro caso posible es que $\alpha\gt\frac\pi2$ (análogamente, se razona para $\beta=\frac\pi2$). En tal caso, la demostración del caso acutángulo se adapta a este caso, teniendo en cuenta ahora que $CHQ$ y $ABQ$ son semejantes por un motivo distinto: ambos son triángulos rectángulos y tienen el mismo ángulo en el vértice común $A$ (opuestos por el vértice).

Queda por analizar el caso en que $\gamma\geq\frac\pi2$. El caso $\gamma=\frac\pi2$ es imposible ya que se tendría que $CH=0$, por lo que supondremos $\gamma\gt\frac\pi2$ (segunda figura). En este caso, $CHQ$ y $ABQ$ vuelven a ser semejantes, lo que nos da de nuevo que $\angle HBQ=\frac{\pi}{4}$. En el triángulo $\angle HBR$, tenemos que $\angle HBR=\frac{\pi}{4}$, $\angle HRB=\frac\pi2$ y $\angle BHR=\pi-\gamma$, luego $\gamma=\frac{3\pi}{4}$.

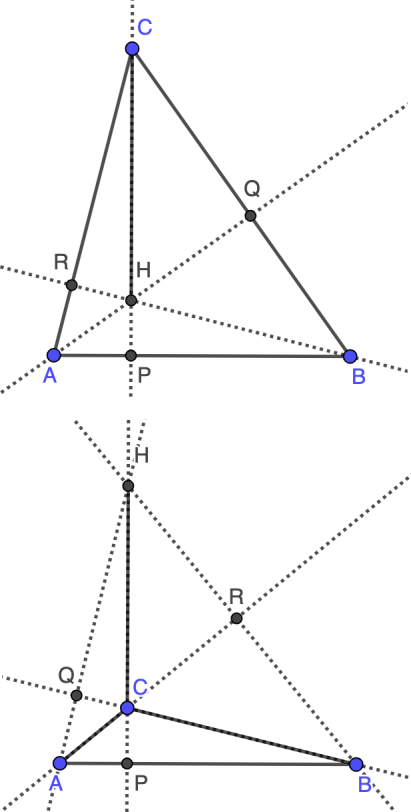
Nota. Este problema es sencillo ya que sólo hay que identificar dos triángulos semejantes en una situación estándar (involucrando al ortocentro). No obstante, se ha marcado con tres estrellas porque es difícil darse cuenta de que puede aparecer una solución distinta si el triángulo es obtusángulo.