Olimpiadas de Matemáticas
Página de preparación y problemas

Solución. Si prolongamos los lados del hexágono, se formarán dos triángulos equiláteros (que contienen al hexágono) ya que sus ángulos interiores son iguales y, por tanto, iguales a $120º$ (ver figura). Si llamamos $a,b,c,d,e,f$ a las longitudes de los lados del hexágono (etiquetados de forma consecutiva), el hecho de que tales triángulos sean equiláteros se traduce en que sus lados son iguales, es decir: \begin{align*} a+b+c=c+d+e=e+f+a,\\ b+c+d=d+e+f=f+a+b. \end{align*} Para llegar a estas igualdades, también hemos usado que al prolongar los lados $a$ y $c$ se forma otro triángulo equilátero de lado $b$ (y lo mismo ocurre para el resto de lados, como se ve en la figura). De las dos ecuaciones anteriores, se llega fácilmente a que \[f-c=b-e=d-a.\] Estas diferencias se pueden suponer positivas, si tomamos $f=6$ como el mayor de los lados en nuestro etiquetado. Como $a,b,c,d,e,f$ son los números del $1$ al $6$ en cierto orden, las diferencias anteriores sólo pueden ser iguales a $1$ y $3$. Además, tras aplicar una simetría axial, podemos suponer que $b$ es mayor que $d$, lo que nos da dos posibles casos:

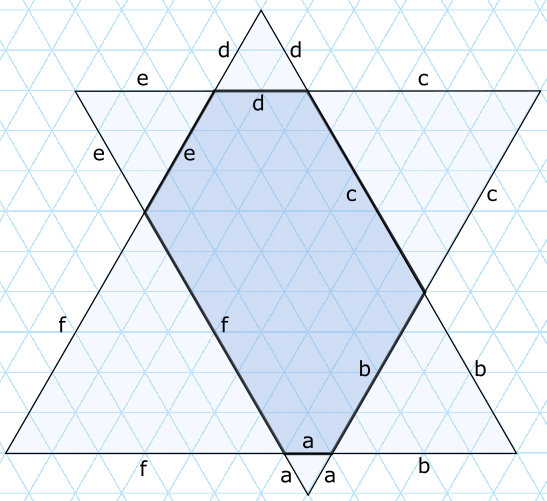
• [Diferencia 3]: $(a,b,c,d,e,f)=(1,5,3,4,2,6)$. El área del hexágono es el área de un triángulo equilátero de lado $a+b+f=12$ menos la suma de las áreas de tres triángulos equiláteros de lados $b=5$, $d=4$ y $f=6$. Como el área de un triángulo equilátero de lado $\ell$ es $\frac{\sqrt{3}}{4}\ell^2$, tenemos que el área del hexágono es \[A=\frac{\sqrt{3}}{4}(12^2-5^2-4^2-6^2)=\frac{67\sqrt{3}}{4}.\]
• [Diferencia 1]: $(a,b,c,d,e,f)=(1,4,5,2,3,6)$. Razonando de forma análoga y teniendo en cuenta que $a+b+f=11$, $b=4$, $d=2$ y $f=6$, llegamos a que \[A=\frac{\sqrt{3}}{4}(11^2-4^2-2^2-6^2)=\frac{65\sqrt{3}}{4}.\]

En la figura, hemos dibujado el segundo de estos dos hexágonos con la ayuda de una malla triangular (el primero se haría de forma similar). Estos son, por tanto, los dos únicos posibles valores del área.