Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 478
OIM, 1992-P6
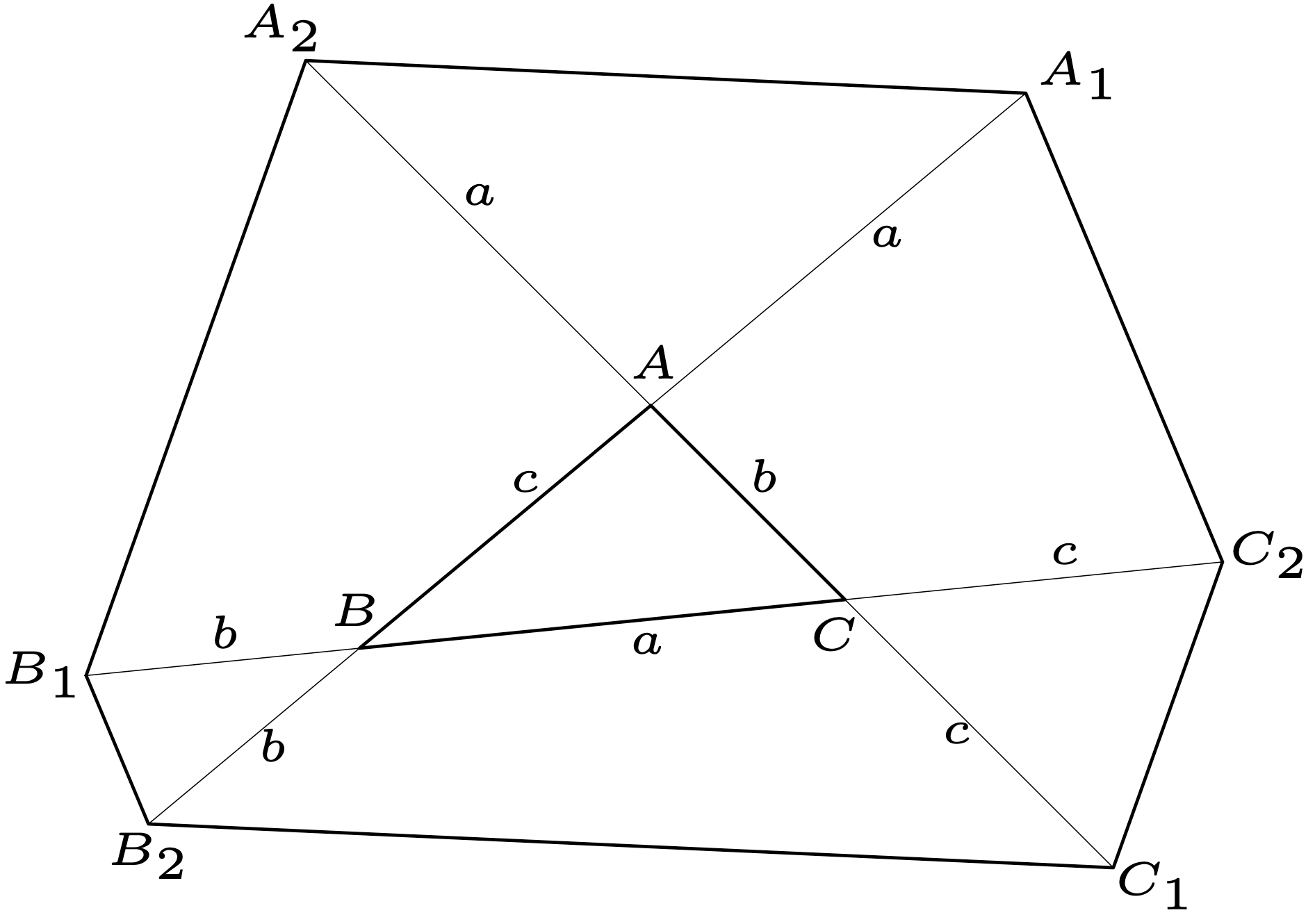
Dado un triángulo $T$ de vértices $A$, $B$ y $C$, construimos un hexágono $H$ de vértices $A_1$, $A_2$, $B_1$, $B_2$, $C_1$ y $C_2$ mediante la prolongación de sus lados según las longitudes indicadas en la figura. Demostrar que el área de $H$ es mayor o igual que $13$ veces el área de $T$.
pistasolución 1info
Pista. Observa que $BA_1C_2$, $BB_1B_2$, $AB_2C_1$, $AA_1A_2$, $CB_1A_2$ y $CC_1C_2$ son seis triángulos isósceles cuyas áreas suman el área de $H$ más dos veces el área de $T$. Esto te debería permitir expresar el área de $H$ en términos de las longitudes de los lados $a,b,c$ y del área de $T$.
Solución. El área de $H$ se puede escribir como
\begin{align*}
\mathrm{Area}(H)&=\mathrm{Area}(AB_2C_1)+\mathrm{Area}(AA_1A_2)+\mathrm{Area}(BA_1C_2)\\
&\quad +\mathrm{Area}(BB_1B_2)+\mathrm{Area}(CB_1A_2)+\mathrm{Area}(CC_1C_2)-2\mathrm{Area}(T).
\end{align*}
Cada uno de los seis triángulos (distintos de $T$) que aparecen en esta expresión son isósceles. Usando que el área de un triángulo es la mitad del producto de dos lados por el seno del ángulo que forman, la suma anterior se puede escribir como
\[\mathrm{Area}(H)=\frac{(b+c)^2+a^2}{2}\mathrm{sen}(\alpha)+\frac{(a+c)^2+b^2}{2}\mathrm{sen}(\beta)+\frac{(a+b)^2+c^2}{2}\mathrm{sen}(\gamma)-2\mathrm{Area}(T),\]
donde $\alpha,\beta,\gamma$ son los ángulos de $T$ en los vértices $A,B,C$, respectivamente. Si tenemos en cuenta que $\mathrm{Area}(T)=\frac{bc}{2}\sin(\alpha)=\frac{ac}{2}\sin(\beta)=\frac{ab}{2}\sin(\gamma)$, podemos eliminar los senos en la expresión anterior, obteniendo
\begin{align*}
\mathrm{Area}(H)&=\left(\frac{(b+c)^2+a^2}{bc}+\frac{(a+c)^2+b^2}{ac}+\frac{(a+b)^2+c^2}{ab}-2\right)\mathrm{Area}(T)\\
&=\left(\frac{b^2+c^2+a^2}{bc}+\frac{a^2+c^2+b^2}{ac}+\frac{a^2+b^2+c^2}{ab}+4\right)\mathrm{Area}(T)\\
&=\left((a^2+b^2+c^2)\left(\frac{1}{ac}+\frac{1}{bc}+\frac{1}{ab}\right)+4\right)\mathrm{Area}(T).
\end{align*}
La desigualdad buscada se deduce entonces de la siguiente
\[\frac{a^2+b^2+c^2}{3}\geq\frac{bc+ac+ab}{3}\geq\frac{3}{\frac{1}{ac}+\frac{1}{bc}+\frac{1}{ab}},\]
donde hemos usado en primer lugar la desigualdad de reordenación y después la desigualdad entre las medias aritmética y armónica.
Nota. La igualdad se alcanza si, y sólo si, el triángulo es equilátero.
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre