Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 491
Encuentra todos los números naturales $n\geq 3$ para los que es posible rellenar un polígono regular de $n$ lados con al menos dos polígonos regulares sin solapamientos (los polígonos del recubrimiento pueden tener distinto número de lados).
pistasolución 1info
Pista. ¿De qué maneras se puede recubrir los vértices del polígono?
Solución. Llamemos $P$ al polígono regular de $n$ lados. Observemos que un vértice $V$ de $P$ es también vértice de los polígonos en que se descompone $P$ de forma que el ángulo interior de $P$ en $V$ es igual a la suma de los ángulos interiores de los polígonos pequeños. Distinguimos dos casos:
- Si en $V$ sólo hay un polígono pequeño $Q$, entonces $Q$ también es un $n$-gono. Como $P$ se descompone en más de un polígono, entonces $Q$ tiene que tener otro vértice $V'$ en un lado de $P$ adyacente a $V$. En el vértice $V'$ deben confluir más polígonos pequeños.
- Si $n\geq 7$, entonces es imposible que esto ocurra porque el ángulo interior del $n$-gono es $180(1-\frac{2}{n})$, que deja un ángulo restante en $V'$ de $\frac{360}{n}\lt 60$, en el que no caben más polígonos regulares ya que el ángulo más pequeño es el del triángulo ($60$).
- Si $n=5$, un pentágono deja un ángulo restante en $V'$ de $\frac{360}{5}=72$. Este tampoco se pude cubrir con ángulos interiores de otros polígonos regulares ya que sólo caben triángulos (y 60 no divide a 72).
- Si $n$ es igual a $3$, $4$ o $6$, entonces sí se puede hacer el recubrimiento, como mostramos más adelante.
- Si en $V$ hay más de un polígono, por el mismo motivo expuesto en el caso anterior, no puede haber $n$-gonos con $n\geq 6$. Además, si colocamos más de dos polígonos en $V$, entonces obtendríamos un ángulo de 180 o más en $V$. Tenemos entonces, las siguientes tres posibilidades para no pasarnos de $180$ en $V$:
- Dos triángulos: nos lleva a un ángulo interior en $V$ de $120$, luego $n=6$. El hexágono sí puede recubrirse como veremos más adelante.
- Un triángulo y un cuadrado: lleva a un ángulo interior en $V$ de $150$, que se corresponde con $n=12$. El dodecácgono sí puede recubrirse, como veremos más adelante.
- Un triángulo y un pentágono: lleva a un ángulo interior en $V$ de $168$, que no es de la forma $180(1-\frac{2}{n})$ ya que obtendríamos $n=\frac{15}{2}\not\in\mathbb{N}$.
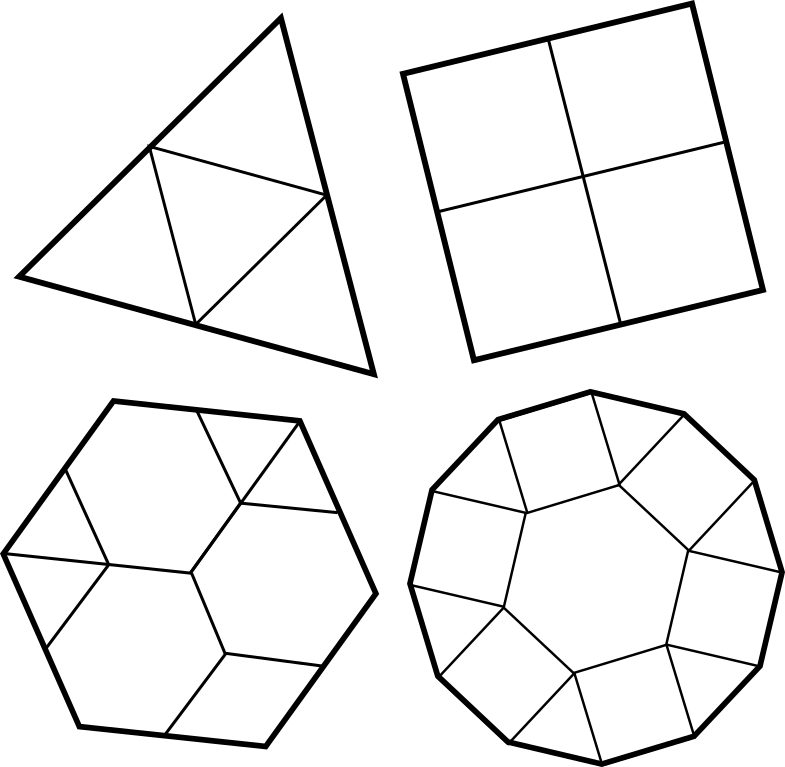
Resta por ver que el triángulo, el cuadrado, el hexágono y el dodecágono pueden recubrirse con polígonos regulares, pero esto es fácil a partir de la discusión anterior, lo que nos da las siguientes figuras:

Nota. La forma de subdividir cada polígono obviamente no es única (por ejemplo, cada una de las piezas de los ejemplos dados puede volver a subdividirse a su vez).
Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre