Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 502
- Probar que si una terna de números positivos $(a,b,c)$ verifica el sistema de ecuaciones \[\left\{\begin{array}{l}a^2+a=b^2,\\b^2+b=c^2,\\c^2+c=a^2,\end{array}\right.\] entonces $(a-b)(b-c)(c-a)=1$.
- Supongamos que $A_1A_2\ldots A_9$ es un eneágono regular tal que \[A_1A_4=1,\qquad A_1A_2=a,\qquad A_1A_3=b,\qquad A_1A_5=c.\] Probar que la terna $(a,b,-c)$ cumple el sistema del apartado anterior.
pistasolución 1info
Pista. El apartado (a) es simple manipulación con un poco de pericia desarrollando el producto $(a-b)(b-c)(c-a)$ (probar que $a+b+c=0$ y $ab+bc+cd=-1$ puede ser útil). Para el apartado (b), usa el teorema de Ptolomeo eligiendo convenientemente cuadriláteros con vértices en los vértices del $n$-gono.
Solución. Para probar el apartado (a), desarrollamos y usamos las ecuaciones para calcular
\begin{align*}
(a-b)(b-c)(c-a)&=(c^2-a^2)b+(b^2-c^2)a+(a^2-b^2)c=-(ab+bc+ac).
\end{align*}
Bastará ver que $ab+bc+ac=-1$. Ahora bien, multiplicando las tres ecuaciones del sistema obtenemos que $abc(a+1)(b+1)(c+1)=a^2b^2c^2$, donde podemos simplificar $abc$ ya que los tres números son no nulos. Esto nos da
\[(a+1)(b+1)(c+1)=abc\Leftrightarrow 1+a+b+c+ab+bc+ac=0.\]
Esto nos da la igualdad deseada ya que, sumando las tres ecuaciones originales, se tiene claramente que $a+b+c=0$.
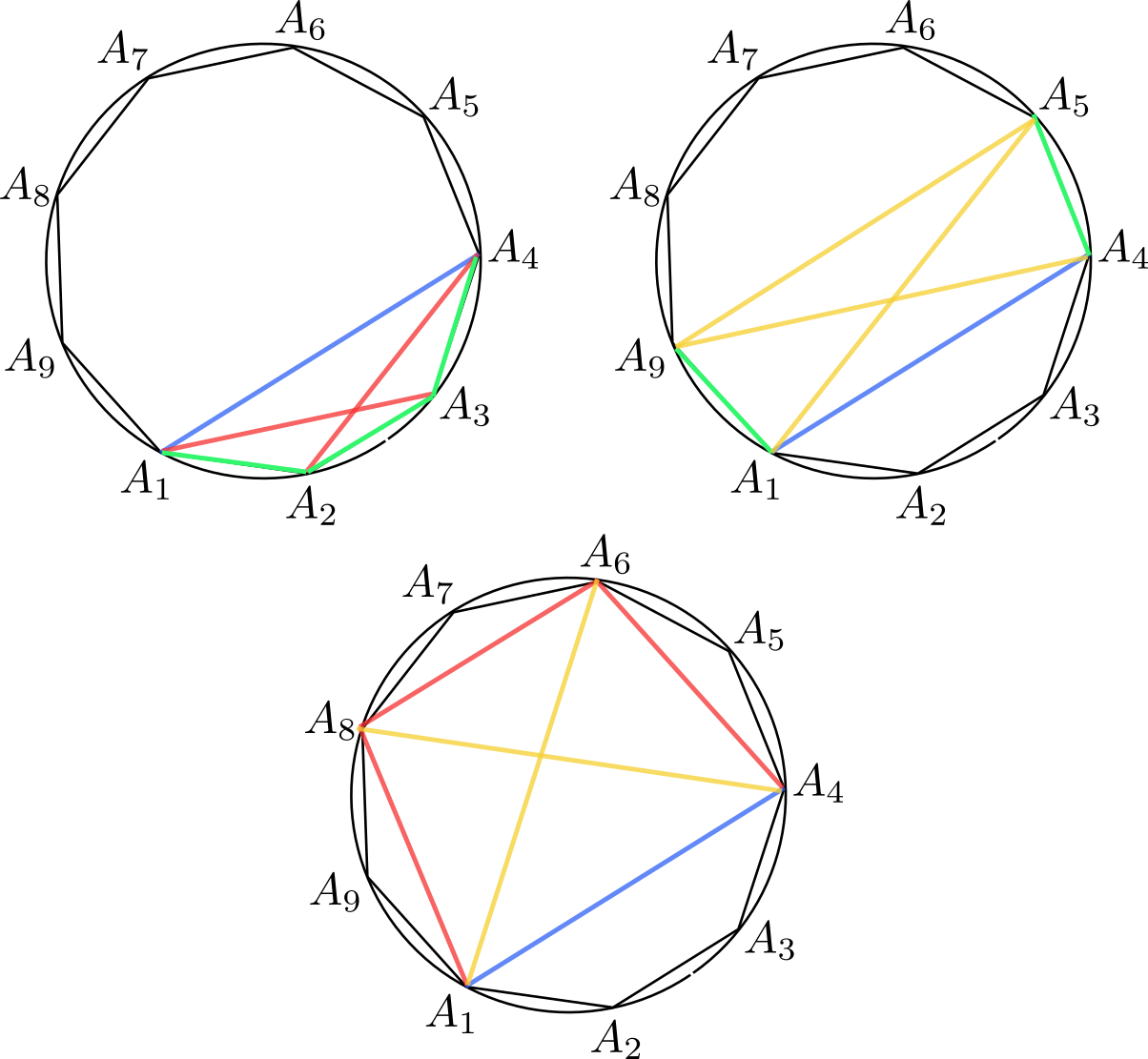
El apartado (b) es bastante estándar a partir del teorema de Ptolomeo para cuadriláteros cíclicos aplicado a cuadriláteros con vértices cuatro de los vértices del eneágono. Observemos que tenemos que probar tres relaciones: (1) $a^2+a=b^2$, (2) $b^2+b=c^2$ y (3) $c^2-c=a^2$ (hemos cambiado $c$ por $-c$ en las ecuaciones del sistema del apartado a). La primera de ellas se sigue de aplicar Ptolomeo al cuadrilátero $A_1A_2A_3A_4$, la segunda al cuadrilátero $A_1A_4A_6A_8$ y la tercera al cuadrilátero $A_1A_4A_5A_9$, como se indica en la figura (los segmentos verdes son iguales a $a$, los rojos a $b$, los azules a $1$ y los amarillos a $c$).

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre