Olimpiadas de Matemáticas
Página de preparación y problemas

Competiciones
| OME Local |
| OME Andaluza |
| OME Nacional |
| OIM |
| IMO |
| EGMO |
| USAMO |
| ASU |
| APMO |
| OMCC |
| Retos UJA |
Buscar problemas
La base de datos contiene 2785 problemas y 1066 soluciones.
Problema 566
OIM, 1987-P6
Sea $ABCD$ un cuadrilátero convexo. Sean $P$ y $Q$ puntos de $AD$ y $BC$, respectivamente, tales que
\[\frac{AP}{PD}=\frac{AB}{DC}=\frac{BQ}{QC}.\]
Demostrar que los ángulos que forma la recta $PQ$ con las rectas $AB$ y $CD$ son iguales.
pistasolución 1info
Pista. Utiliza la proporcionalidad del enunciado para encontrar dos cuadriláteros semejantes, aunque para ello tendrás que dibujar algunos puntos nuevos
Solución. Construimos puntos $P'$ y $Q'$ sobre la recta $PQ$ tales que $PD=P'D$ y $CQ=C'Q$. Supondremos que $P\neq P'$ y $Q\neq Q'$ a menos que $AD$ o $BC$ sean perpendiculares a $PQ$. Observamos que $pp'D$ y $QQ'C$ son isósceles, luego se tiene que $\angle APQ=\angle P'PD=\angle Q'P'D$ y $\angle BQP=\angle Q'QC=\angle P'Q'C$. Esta igualdad de ángulos junto con las proporciones dadas en el enunciado nos dicen que $ABQP$ y $DCQ'P'$ son cuadriláteros semejantes (indicados en rojo y verde en la figura. Por tanto, el ángulo que forman los pares de lados opuestos $AB$ y $PQ$ en $ABQP$ es el mismo que el que forman los lados homólogos $CD$ y $P'Q'$ en $DCQ'P'$. Dicho de otra forma, cuando prolongamos los estos lados, obtenemos triángulos semejantes $APX$ y $DP'Y$ (representados en azul), siendo $X$ la intersección de $PQ$ y $AB$ e $Y$ la intersección de $PQ$ y $CD$. Esto concluye la demostración ya que nos dice que $\angle AXP=\angle DYP$.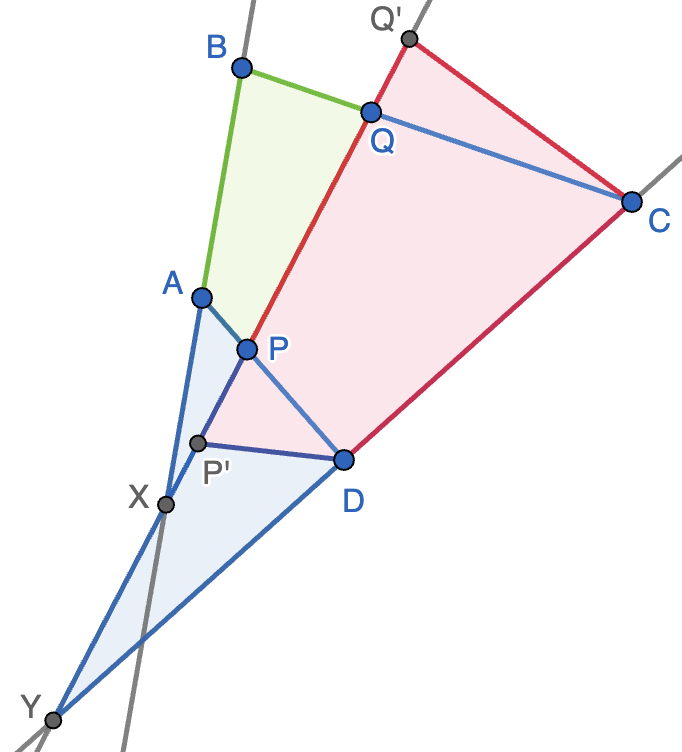

Si crees que el enunciado contiene un error o imprecisión o bien crees que la información sobre la procedencia del problema es incorrecta, puedes notificarlo usando los siguientes botones:
Informar de error en enunciado Informar de procedencia del problema
Informar de error en enunciado Informar de procedencia del problema
José Miguel Manzano © 2010-2026. Esta página ha sido creada mediante software libre